14.4 Momentum transfer by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
14.4 Momentum transfer
The rate of change of momentum
As with conservation of energy, we need a way to measure and calculate the transfer of momentum into or out of a system when the system is not closed. In the case of energy, the answer was rather complicated, and entirely different techniques had to be used for measuring the transfer of mechanical energy (work) and the transfer of heat by conduction. For momentum, the situation is far simpler.
In the simplest case, the system consists of a single object acted on by a constant external force. Since it is only the object's velocity that can change, not its mass, the momentum transferred is
which with the help of `a=F"/"m` and the constant-acceleration equation `a=Deltav"/"Deltat` becomes
`Deltap=maDeltat`
 `=FDeltat`.
`=FDeltat`.
Thus the rate of transfer of momentum, i.e., the number of `kg*m"/"s` absorbed per second, is simply the external force,
`F=(Deltap)/(Deltat)`.
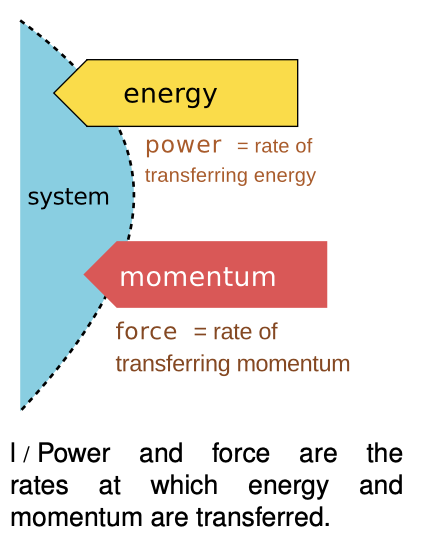
[relationship between the force on an object and the rate of change of its momentum; valid only if the force is constant] This is just a restatement of Newton's second law, and in fact Newton originally stated it this way. As shown in figure l, the relationship between force and momentum is directly analogous to that between power and energy.
The situation is not materially altered for a system composed of many objects. There may be forces between the objects, but the internal forces cannot change the system's momentum. (If they did, then removing the external forces would result in a closed system that could change its own momentum, like the mythical man who could pull himself up by his own bootstraps. That would violate conservation of momentum.) The equation above becomes
`F_"total"=(Deltap_"total")/(Deltat)`.
 [relationship between the total external force on a system and the rate of change of its total momentum; valid only if the force is constant]
[relationship between the total external force on a system and the rate of change of its total momentum; valid only if the force is constant]
Example 14: Walking into a lamppost
`=>` Starting from rest, you begin walking, bringing your momentum up to `100 kg*m"/"s`. You walk straight into a lamppost. Why is the momentum change of `-100 kg*m"/"s` caused by the lamppost so much more painful than the change of `+100 kg*m"/"s` when you started walking?
`=>` The situation is one-dimensional, so we can dispense with the vector notation. It probably takes you about 1 s to speed up initially, so the ground's force on you is `F=Deltap"/"Deltatapprox100 N`. Your impact with the lamppost, however, is over in the blink of an eye, say 1/10 s or less. Dividing by this much smaller `Deltat` gives a much larger force, perhaps thousands of newtons. (The negative sign simply indicates that the force is in the opposite direction.)
This is also the principle of airbags in cars. The time required for the airbag to decelerate your head is fairly long, the time required for your face to travel 20 or 30 cm. Without an airbag, your face would hit the dashboard, and the time interval would be the much shorter time taken by your skull to move a couple of centimeters while your face compressed. Note that either way, the same amount of mechanical work has to be done on your head: enough to eliminate all its kinetic energy.
Example 15: Ion drive for spacecraft
 `=>` The ion drive of the Deep Space 1 spacecraft, pictured on page 357 and discussed in example 2, produces a thrust of 90 mN (millinewtons). It carries about 80 kg of reaction mass, which it ejects at a speed of 30,000 m/s. For how long can the engine continue supplying this amount of thrust before running out of reaction mass to shove out the back?
`=>` The ion drive of the Deep Space 1 spacecraft, pictured on page 357 and discussed in example 2, produces a thrust of 90 mN (millinewtons). It carries about 80 kg of reaction mass, which it ejects at a speed of 30,000 m/s. For how long can the engine continue supplying this amount of thrust before running out of reaction mass to shove out the back?
`=>` Solving the equation `F=(Deltap)/(Deltat)` for the unknown `Deltat`, and treating force and momentum as scalars since the problem is one-dimensional, we find
`Deltat=(Deltap)/F`
`=(m_"exhaust"Deltav_"exhaust")/F`
`=((80 kg)(30,000 m/s))/(0.090 N)`
`=2.7×10^7 s`
`=300 days`
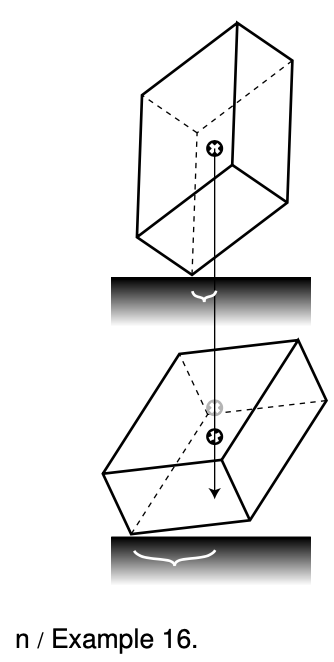
Example 16: A toppling box
If you place a box on a frictionless surface, it will fall over with a very complicated motion that is hard to predict in detail. We know, however, that its center of mass moves in the same direction as its momentum vector points. There are two forces, a normal force and a gravitational force, both of which are vertical. (The gravitational force is actually many gravitational forces acting on all the atoms in the box.) The total force must be vertical, so the momentum vector must be purely vertical too, and the center of mass travels vertically. This is true even if the box bounces and tumbles. [Based on an example by Kleppner and Kolenkow.]
 The area under the force-time graph
The area under the force-time graph
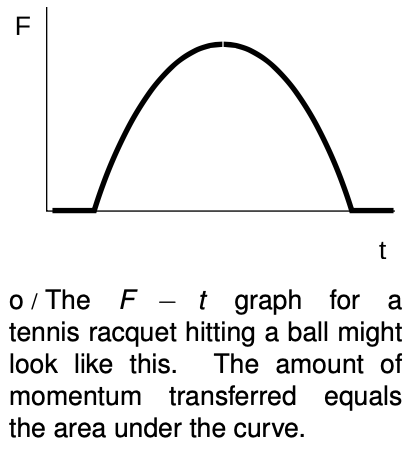
Few real collisions involve a constant force. For example, when a tennis ball hits a racquet, the strings stretch and the ball flattens dramatically. They are both acting like springs that obey Hooke's law, which says that the force is proportional to the amount of stretching or flattening. The force is therefore small at first, ramps up to a maximum when the ball is about to reverse directions, and ramps back down again as the ball is on its way back out. The equation `F=Deltap"/"Deltat`, derived under the assumption of constant acceleration, does not apply here, and the force does not even have a single well-defined numerical value that could be plugged in to the equation.
As with similar-looking equations such as `v=Deltap"/"Deltat`, the equation `F=Deltap"/"Deltat` is correctly generalized by saying that the force is the slope of the`p-t` graph.
Conversely, if we wish to find `Deltap` from a graph such as the one in figure o, one approach would be to divide the force by the mass of the ball, rescaling the `F` axis to create a graph of acceleration versus time. The area under the acceleration-versus-time graph gives the change in velocity, which can then be multiplied by the mass to find the change in momentum. An unnecessary complication was introduced, however, because we began by dividing by the mass and ended by multiplying by it. It would have made just as much sense to find the area under the original `F-t` graph, which would have given us the momentum change directly.
Discussion Question
A Many collisions, like the collision of a bat with a baseball, appear to be instantaneous. Most people also would not imagine the bat and ball as bending or being compressed during the collision. Consider the following possibilities:
- The collision is instantaneous.
- The collision takes a finite amount of time, during which the ball and bat retain their shapes and remain in contact.
- The collision takes a finite amount of time, during which the ball and bat are bending or being compressed.
How can two of these be ruled out based on energy or momentum considerations?
14.4 Momentum transfer by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.