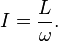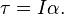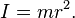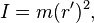The Moment of Inertia calculator has numerous equations for the moment of inertial for different shapes around different axis.
Description
The Moment of inertia calculator has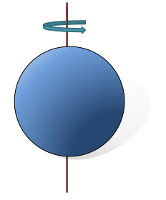
Solid sphere around diameterequations for calculating the moment of inertia for different shapes including:
- Annulus
- Box
- Circular Cone
- Circular Plate
- Ellipsoid
- Solid Sphere
- Hollow Sphere
- Cylinder
- Hollow Cylinder
Moments of Inertia
Moment of inertia is the mass property of a rigid body that determines the torque needed for a desired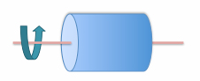
Circular cylinder around the axis angular acceleration about an axis of rotation. Moment of inertia depends on the shape of the body and may be different around different axes of rotation. A larger moment of inertia around a given axis requires more torque to increase the rotation, or to stop the rotation, of a body about that axis. Moment of inertia depends on the amount and distribution of its mass, and can be found through the sum of moments of inertia of the masses making up the whole object, under the same conditions. For example, if ma + mb = mc, then Ia + Ib = Ic. In classical mechanics, moment of inertia may also be called mass moment of inertia, rotational inertia, polar moment of inertia, or the angular mass.
For planar movement of a body, the trajectories of all of its points lie in parallel planes, and the rotation occurs only about an axis perpendicular to this plane. In this case, the body has a single moment of inertia, which is measured around this axis.
For spatial movement of a body, the moment of inertia is defined by its symmetric 3 × 3 inertia matrix.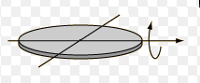
circular plate The inertia matrix is often described as a symmetric rank two tensor, having six independent components. The inertia matrix includes off-diagonal terms called products of inertia that couple torque around one axis to angular acceleration about another axis. Each body has a set of mutually perpendicular axes, called principal axes, for which the off-diagonal terms of the inertia matrix are zero, and a torque around a principal axis only affects the acceleration about that axis.
Introduction
When a body is rotating around an axis, a torque must be applied to change its angular momentum. The amount of torque needed for any given change in angular momentum is proportional to the size of that change. Moment of inertia may be expressed in terms of kilogram-square meters (kg·m2) in SI units and pound-square feet (lbm·ft2) in imperial or US units.
In 1673 Christiaan Huygens introduced this parameter in his study of the oscillation of a body hanging from a pivot, known as a compound pendulum. The term moment of inertia was introduced by Leonhard Euler in his book Theoria motus corporum solidorum seu rigidorum in 1765, and it is incorporated into Euler's second law.
The natural frequency of oscillation of a compound pendulum is obtained from the ratio of the torque imposed by gravity on the mass of the pendulum to the resistance to acceleration defined by the moment of inertia. Comparison of this natural frequency to that of a simple pendulum consisting of a single point of mass provides a mathematical formulation for moment of inertia of an extended body.
Moment of inertia also appears in momentum, kinetic energy, and in Newton's laws of motion for a rigid body as a physical parameter that combines its shape and mass. There is an interesting difference in the way moment of inertia appears in planar and spatial movement. Planar movement has a single scalar that defines the moment of inertia, while for spatial movement the same calculations yield a 3 × 3 matrix of moments of inertia, called the inertia matrix or inertia tensor.
The moment of inertia of a rotating flywheel is used in a machine to resist variations in applied torque to smooth its rotational output. The moment of inertia of an airplane about its longitudinal, horizontal and vertical axes determines how steering forces on the control surfaces of its wings, elevators and tail affect the plane in roll, pitch and yaw.
Definition
Moment of inertia I is defined as the ratio of the angular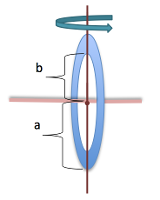
Annulus around the diameter momentum L of a system to its angular velocity ω around a principal axis, that is
If the momentum of a system is constant, then as the moment of inertia gets smaller, the angular velocity must increase. This occurs when spinning figure skaters pulls in their outstretched arms or divers move from a straight position to a tuck position during a dive.
If the shape of the body does not change, then its moment of inertia appears in Newton's law of motion as the ratio of an applied torque τ on a body to the angular acceleration α around a principal axis, that is
For a simple pendulum, this definition yields a formula for the moment of inertia I in terms of the mass m of the pendulum and its distance r from the pivot point as,
Thus, moment of inertia depends on both the mass m of a body and its geometry, or shape, as defined by the distance r to the axis of rotation.
This simple formula generalizes to define moment of inertia for an arbitrarily shaped body as the sum of all the elemental point masses dm each multiplied by the square of its perpendicular distance r to an axis S .
In general, given an object of mass m, an effective radius r′ can be defined for an arbitrary axis of interest, with such a value that its moment of inertia is
regardless of any symmetry that could justify, or not, defining a radius for that object.
Partner Institutions
See Also
- Mass Weight - calculator with equations and data to calculate the mass of different geometric shapes.
- Moment of Inertia - Basic equation for moment of inertia.
- Sphere Calculator - calculator with equations and data related to spheres.
- Vector (3D) - Vector calculator in 3D space.
- Pendulum - Calculator with equations related to the pendulum.
- Stress & Strain - Engineering calculator with stress and strain equations.
Reference
- Wikipedia - http://en.wikipedia.org/wiki/Moment_of_inertia