The Ellipse Calculator has formulas and 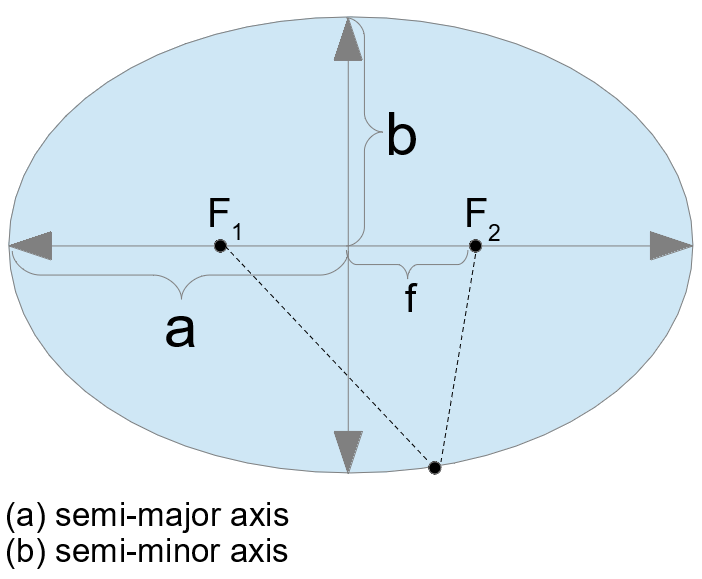 The Ellipseinformation related to the ellipse including formulas for the following:
The Ellipseinformation related to the ellipse including formulas for the following:
- Area of Ellipse: this computes the area of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Rumanujan's Circumference of an Ellipse 1 this first of two of Rumanujan's approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Rumanujan's Circumference of an Ellipse 2this is the second Rumanujan approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Circumference of an Ellipse (other) this is another common estimation of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Eccentricity of an Ellipse this computes the eccentricity of an ellipse which is based on the ratios of the semi-major axis (a) and the semi-minor axis (b).
- Linear Eccentricity of an Ellipse (f) this computes the distance from the center to either foci (f), which is the linear eccentricity of an ellipse. This is based on the semi-major axis (a) and the semi-minor axis (b).
- Mean Radius of an Ellipse this compute the mean radius of an ellipse. This would define a circle with the same approximate area, based on the ellipse's semi-major axis (a) and the semi-minor axis (b).
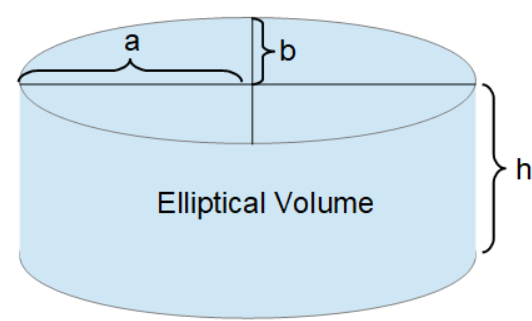
- Elliptical Volume - this computes the volume of a column with an elliptical base.
- Ellipsoid Calculator - This the volume, mass and surface area of ellipse based (ellipsoidal) 3D shapes
UNITS: The input lengths for the semi-major (a) and semi-minor (b) axes have a default unit of meters. However, the user can sellect any of the other length units provided (e.g. inches to light-years) via the pull-down menu, and vCalc will automatically make the conversions in the calculations. The answers are either in meters or square meters depending on the formula. However, these too can be automatically converted to other length or area (e.g. square miles, acres) via the pull-down menu next to the answer.
The Ellipse
In mathematics, an ellipse is a curve on a plane surrounding two focal points such that a straight line drawn from one of the focal points to any point on the curve and then back to the other focal point has the same length for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse that has both focal points at the same location. The shape of an ellipse (how 'elongated' it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle) to arbitrarily close to but less than 1.
Ellipses are the closed type of conic section: a plane curve that results from the intersection of a cone by a plane. Ellipses have many similarities with the other two forms of conic sections: the parabolas and the hyperbolas, both of which are open and unbounded. The cross section of a cylinder is an ellipse if it is sufficiently far from parallel to the axis of the cylinder.ellipse - conic section
Analytically, an ellipse can also be defined as the set of points such that the ratio of the distance of each point on the curve from a given point (called a focus or focal point) to the distance from that same point on the curve to a given line (called the directrix) is a constant, called the eccentricity of the ellipse.
Ellipses are common in physics, astronomy and engineering. For example, the orbits of the planets are ellipses with the Sun at one of the focal points. The same is true for moons orbiting planets and all other systems having two astronomical bodies. The shape of planets and stars are often well described by ellipsoids. Ellipses also arise as images of a circle under parallel projection and the bounded cases of perspective projection, which are simply intersections of the projective cone with the plane of projection. It is also the simplest Lissajous figure, formed when the horizontal and vertical motions are sinusoids with the same frequency. A similar effect leads to elliptical polarization of light in optics.
The name, ἔλλειψις (élleipsis, "omission"), was given by Apollonius of Perga in his Conics, emphasizing the connection of the curve with "application of areas".
Elements of an Ellipse
Ellipses have two mutually perpendicular axes about which the ellipse is symmetric. These axes intersect at the center of the ellipse due to this symmetry. The larger of these two axes, which corresponds to the largest distance between antipodal points on the ellipse, is called the major axis. (On the figure to the right it is represented by the line segment between the point labeled −a and the point labeled a.) The smaller of these two axes, and the smallest distance across the ellipse, is called the minor axis. (On the figure to the right it is represented by the line segment between the point labeled −b to the point labeled b.)
The semi-major axis (denoted by a in the figure) and the semi-minor axis (denoted by b in the figure) are one half of the major and minor axes, respectively. These are sometimes called (especially in technical fields) the major and minor semi-axes, the major and minor semiaxes, or major radius and minor radius.
The four points 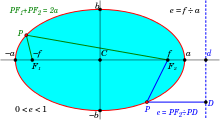 elements of an ellipse where these axes cross the ellipse are the vertices and are marked as a, −a, b, and −b. In addition to being at the largest and smallest distance from the center, these points are where the curvature of the ellipse is maximum and minimum.
elements of an ellipse where these axes cross the ellipse are the vertices and are marked as a, −a, b, and −b. In addition to being at the largest and smallest distance from the center, these points are where the curvature of the ellipse is maximum and minimum.
The two foci (plural of focus and the term focal points is also used) of an ellipse are two special points F1 and F2 on the ellipse's major axis that are equidistant from the center point. The sum of the distances from any point P on the ellipse to those two foci is constant and equal to the major axis (PF1 + PF2 = 2a). (On the figure to the right this corresponds to the sum of the two green lines equaling the length of the major axis that goes from −a to a.)
The distance to the focal point from the center of the ellipse is sometimes called the linear eccentricity, f, of the ellipse. Here it is denoted by f, but it is often denoted by c. Due to the Pythagorean theorem and the definition of the ellipse explained in the previous paragraph: f2 = a2 −b2.
A second equivalent method of constructing an ellipse using a directrix is shown on the plot as the three blue lines. (See the Directrix section of this article for more information about this method). The dashed blue line is the directrix of the ellipse shown.
The eccentricity of an ellipse, usually denoted by ε or e, is the ratio of the distance between the two foci, to the length of the major axis or e = 2f/2a = f/a. For an ellipse the eccentricity is between 0 and 1 (0 < e < 1). When the eccentricity is 0 the foci coincide with the center point and the figure is a circle. As the eccentricity tends toward 1, the ellipse gets a more elongated shape. It tends towards a line segment (see below) if the two foci remain a finite distance apart and a parabola if one focus is kept fixed as the other is allowed to move arbitrarily far away. The eccentricity is also equal to the ratio of the distance (such as the (blue) line PF2) from any particular point on an ellipse to one of the foci to the perpendicular distance to the directrix from the same point (line PD), e = PF2/PD.
Drawing Ellipses
Pins-and-string method
The characterization of an ellipse as the locus of points so Pins and string methodthat sum of the distances to the foci is constant leads to a method of drawing one using two drawing pins, a length of string, and a pencil. In this method, pins are pushed into the paper at two points which will become the ellipse's foci. A string tied at each end to the two pins and the tip of a pen is used to pull the loop taut so as to form a triangle. The tip of the pen will then trace an ellipse if it is moved while keeping the string taut. Using two pegs and a rope, this procedure is traditionally used by gardeners to outline an elliptical flower bed; thus it is called the gardener's ellipse.
Pins and string methodthat sum of the distances to the foci is constant leads to a method of drawing one using two drawing pins, a length of string, and a pencil. In this method, pins are pushed into the paper at two points which will become the ellipse's foci. A string tied at each end to the two pins and the tip of a pen is used to pull the loop taut so as to form a triangle. The tip of the pen will then trace an ellipse if it is moved while keeping the string taut. Using two pegs and a rope, this procedure is traditionally used by gardeners to outline an elliptical flower bed; thus it is called the gardener's ellipse.

Trammel method
An ellipse can also be drawn using a ruler, a set square, and a pencil: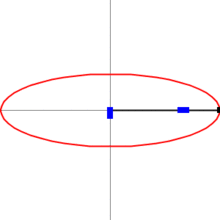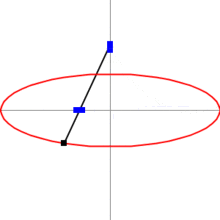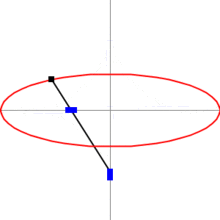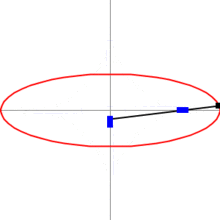
-
Draw two perpendicular lines
M,
N on the paper; these will be the major (
M) and minor (
N) axes of the ellipse. Mark three points
A,
B,
C on the ruler.
A->C being the length of the semi-major axis and
B->C the length of the semi-minor axis. With one hand, move the ruler on the paper, turning and sliding it so as to keep point
A always on line
N, and
B on line
M. With the other hand, keep the pencil's tip on the paper, following point
C of the ruler. The tip will trace out an ellipse.
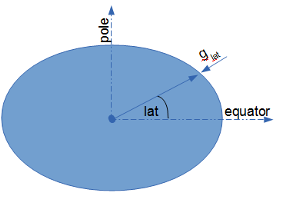 Earth Oblateness
Earth Oblateness
The trammel of Archimedes, or ellipsograph, is a mechanical device that implements this principle. The ruler is replaced by a rod with a pencil holder (point C) at one end, and two adjustable side pins (points A and B) that slide into two perpendicular slots cut into a metal plate. The mechanism can be used with a router to cut ellipses from board material. The mechanism is also used in a toy called the "nothing grinder".
Ellipses in Science
Elliptical Orbits
The ellipse is observed in many natural phenomenon. One of the most famous was the critical observation by Johannes Kepler that planets orbited the Sun in elliptical paths and not circular orbits. As the story goes, Kepler was using the observation data of the orbit of Mars as measured by Tycho Brahe, who was famous for his accuracy. Fortunately, Mar's orbit is the most eccentric (elliptical) of the inner planets, and the evidence indisputably pointed toward elliptical orbits.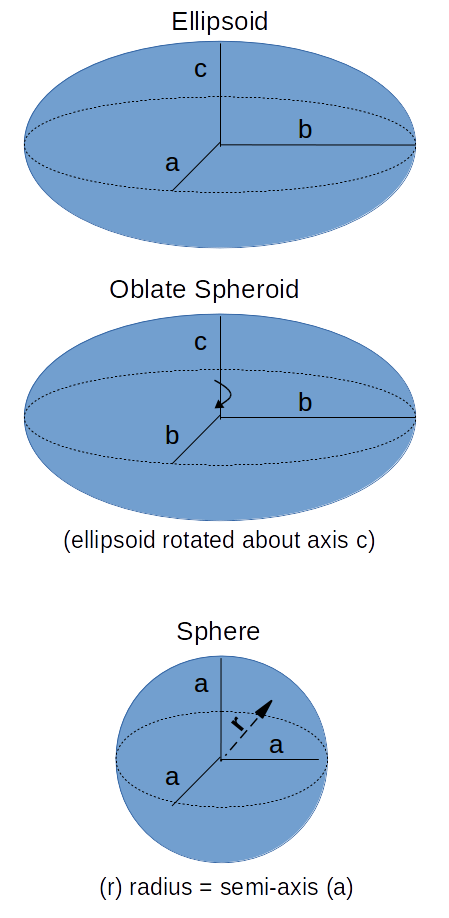
Ellipsoid and Oblate Spheroid
The ellipse can be observed (approximately) in a slice of the Earth through the poles. Gravity uniformly pulls the matter of the Earth into a spherical body. However, the rotation of the earth and the resulting centrifugal force radiating outward creates a bulging effect at the equator. The net result is an elliptical shape of the Earth's cross-section and more mass and consequently, more gravitational acceleration near the equator. (See International Gravity Formula).
Ellipsoid Calculator
- Ellipsoid - Volume computes the volume of an ellipsoid based on the length of the three semi-axes (a, b, c)
- Ellipsoid - Surface Area computes the surface area of an ellipsoid based on the length of the three semi-axes (a, b, c)
- Ellipsoid - Mass or Weight computes the mass or weight of an ellipsoid based on the length of the three semi-axes (a, b, c) and the mean density.
- Oblate Spheroid - Volume computes the volume of an Oblate Spheroid based on the length of the two semi-axes (b, c)
- Oblate Spheroid- Surface Area computes the surface area of an Oblate Spheroid based on the length of the two semi-axes (b, c)
- Oblate Spheroid- Mass or Weight computes the mass or weight of an Oblate Spheroid based on the length of the two semi-axes (b, c) and the mean density.
See Also
- Cone Calculator - Equations related to conic shaped objects.
- Cylinder Calculator - Equations for cylinders
- Sphere Calculator - Equations related to spheres.
- Circle Calculator - Equations related to circles
- Ellipse Calculator - Equations related to ellipses
- Geometer (3D) - Equations related to various shapes in 3D
- Frustum - Equations related to the frustums of various objects
- Moments of Inertia - Equations related to the Moments of Inertia of different shapes about different axes.
Reference
- wikipedia - http://en.wikipedia.org/wiki/Ellipse
- Animation of the elipse is from: https://lh6.googleusercontent.com/-Gf58RKtiaoI/U4cZL6DxLzI/AAAAAAAAAE4/ymfjN-8bPOA/w506-h285/ellipse.gif