Homework Problems by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

	vCalc Formulas
Step	Action	Calculator
1	Altitude Drop Before Parachute Opens	Altitude (`y`)
2	Honeybee Position	`x`

Homework Problems

1. The graph shows the motion of a car stuck in stop-and-go freeway traffic. (a) If you only knew how far the car had gone during this entire time period, what would you think its velocity was? (b) What is the car's maximum velocity? (answer check available at lightandmatter.com

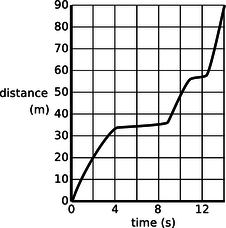 ac / Problem 1. 

2. (a) Let `theta` be the latitude of a point on the Earth's surface. Derive an algebra equation for the distance, `L`, traveled by that point during one rotation of the Earth about its axis, i.e., over one day, expressed in terms of `theta`and `R`, the radius of the earth. Check: Your equation should give `L`=0 for the North Pole.
(b) At what speed is Fullerton, at latitude `theta`=34°, moving with the rotation of the Earth about its axis? Give your answer in units of mi/h. [See the table in the back of the book for the relevant data.](answer check available at lightandmatter.com)

 ad / Problem 7.

3. A person is parachute jumping. During the time between when she leaps out of the plane and when she opens her chute, her altitude is given by the equation

`y=(10000 m)?(50 m"/"s)[t+(5.0 s)e^(?t"/"5.0 s)]`.

Find her velocity at `t`=7.0 s. (This can be done on a calculator, without knowing calculus.) Because of air resistance, her velocity does not increase at a steady rate as it would for an object falling in vacuum. (answer check available at lightandmatter.com)

  ae / Problem 8.

4. (solution in the pdf version of the book) A light-year is a unit of distance used in astronomy, and defined as the distance light travels in one year. The speed of light is 3.0×`10^8` m/s. Find how many meters there are in one light-year, expressing your answer in scientific notation.

5. (solution in the pdf version of the book) You're standing in a freight train, and have no way to see out. If you have to lean to stay on your feet, what, if anything, does that tell you about the train's velocity? Explain.

6. A honeybee's position as a function of time is given by `x=10t?t^3`, where `t` is in seconds and `x` in meters. What is its velocity at `t`=3.0s? (answer check available at lightandmatter.com) ?

7. (solution in the pdf version of the book) The figure shows the motion of a point on the rim of a rolling wheel. (The shape is called a cycloid.) Suppose bug A is riding on the rim of the wheel on a bicycle that is rolling, while bug B is on the spinning wheel of a bike that is sitting upside down on the floor. Bug A is moving along a cycloid, while bug B is moving in a circle. Both wheels are doing the same number of revolutions per minute. Which bug has a harder time holding on, or do they find it equally difficult?

8. Peanut plants fold up their leaves at night. Estimate the top speed of the tip of one of the leaves shown in the figure, expressing your result in scientific notation in SI units. (answer check available at lightandmatter.com)

9. (a) Translate the following information into symbols, using the notation with two subscripts introduced in section 2.5. Eowyn is riding on her horse at a velocity of 11 m/s. She twists around in her saddle and fires an arrow backward. Her bow fires arrows at 25 m/s. (b) Find the velocity of the arrow relative to the ground.

 
ag / Problem 16. 

10. (solution in the pdf version of the book) Our full discussion of two- and three-dimensional motion is postponed until the second half of the book, but here is a chance to use a little mathematical creativity in anticipation of that generalization. Suppose a ship is sailing east at a certain speed `v`, and a passenger is walking across the deck at the same speed `v`, so that his track across the deck is perpendicular to the ship's center-line. What is his speed relative to the water, and in what direction is he moving relative to the water?

1. 1. Freddi Fish`(TM)` has a position as a function of time given by `x=a"/"(b+t^2)`. (a) Infer the units of the constants `a` and `b`

 
ah / Problem 17. 

 (b) Find her maximum speed. (c) Check that your answer has the right units. (answer check available at lightandmatter.com) ?

12. Driving along in your car, you take your foot off the gas, and your speedometer shows a reduction in speed. Describe a frame of reference in which your car was speeding up during that same period of time. (The frame of reference should be defined by an observer who, although perhaps in motion relative to the earth, is not changing her own speed or direction of motion.)

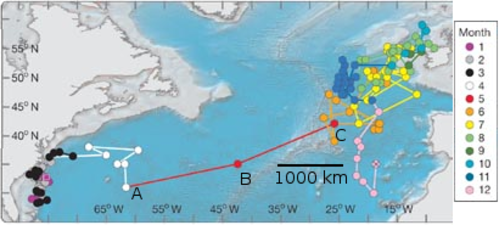 af / Problem 13.

13. The figure shows the motion of a bluefin tuna, as measured by a radio tag (Block et al., Nature, v. 434, p. 1121, 2005), over the course of several years. Until this study, it had been believed that the populations of the fish in the eastern and western Atlantic were separate, but this particular fish was observed to cross the entire Atlantic Ocean, from Virginia to Ireland. Points A, B, and C show a period of one month, during which the fish made the most rapid progress. Estimate its speed during that month, in units of kilometers per hour.(answer check available at lightandmatter.com)

14. Sometimes doors are built with mechanisms that automatically close them after they have been opened. The designer can set both the strength of the spring and the amount of friction. If there is too much friction in relation to the strength of the spring, the door takes too long to close, but if there is too little, the door will oscillate. For an optimal design, we get motion of the form `x=cte^(?bt)`, where `x` is the position of some point on the door, and `c` and `b` are positive constants. (Similar systems are used for other mechanical devices, such as stereo speakers and the recoil mechanisms of guns.) In this example, the door moves in the positive direction up until a certain time, then stops and settles back in the negative direction, eventually approaching `x=0`. This would be the type of motion we would get if someone flung a door open and the door closer then brought it back closed again. (a) Infer the units of the constants `b` and `c`.
 (b) Find the door's maximum speed (i.e., the greatest absolute value of its velocity) as it comes back to the closed position.(answer check available at lightandmatter.com)
 (c) Show that your answer has units that make sense. ?

15. At a picnic, someone hands you a can of beer. The ground is uneven, and you don't want to spill your drink. You reason that it will be more stable if you drink some of it first in order to lower its center of mass. How much should you drink in order to make the center of mass as low as possible? [Based on a problem by Walter van B. Roberts and Martin Gardner.]

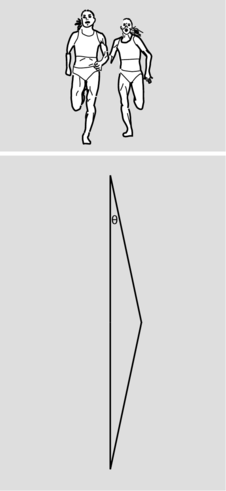
16. In running races at distances of 800 meters and longer, runners do not have their own lanes, so in order to pass, they have to go around their opponents. Suppose we adopt the simplified geometrical model suggested by the figure, in which the two runners take equal times to trace out the sides of an isoceles triangle, deviating from parallelism by the angle `theta`. The runner going straight runs at speed `v`, while the one who is passing must run at a greater speed. Let the difference in speeds be `Deltav`.
 (a) Find `Deltav` in terms of `v` and `theta`.(answer check available at lightandmatter.com)
 (b) Check the units of your equation using the method shown in example 1 on p. 27.
 (c) Check that your answer makes sense in the special case where `theta`=0, i.e., in the case where the runners are on an extremely long straightaway.
 (d) Suppose that `theta`=1.0 degrees, which is about the smallest value that will allow a runner to pass in the distance available on the straightaway of a track, and let `v`=7.06 m/s, which is the women's world record pace at 800 meters. Plug numbers into your equation from part a to determine `Deltav`, and comment on the result.(answer check available at lightandmatter.com)

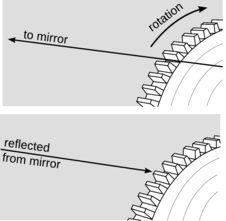
17. In 1849, Fizeau carried out the first terrestrial measurement of the speed of light; previous measurements by Roemer and Bradley had involved astronomical observation. The figure shows a simplified conceptual representation of Fizeau's experiment. A ray of light from a bright source was directed through the teeth at the edge of a spinning cogwheel. After traveling a distance `L`, it was reflected from a mirror and returned along the same path. The figure shows the case in which the ray passes between two teeth, but when it returns, the wheel has rotated by half the spacing of the teeth, so that the ray is blocked. When this condition is achieved, the observer looking through the teeth toward the far-off mirror sees it go completely dark. Fizeau adjusted the speed of the wheel to achieve this condition and recorded the rate of rotation to be f'>f rotations per second. Let the number of teeth on the wheel be `n`.
 (a) Find the speed of light `c` in terms of `L`, `n`, and `f`.(answer check available at lightandmatter.com)
 (b) Check the units of your equation using the method shown in example 1 on p. 27. (Here f'>f's units of rotations per second should be taken as inverse seconds, `s^(?1), since the number of rotations in a second is a unitless count.)
 (c) Imagine that you are Fizeau trying to design this experiment. The speed of light is a huge number in ordinary units. Use your equation from part a to determine whether increasing `c` requires an increase in `L`, or a decrease. Do the same for `n` and `f`. Based on this, decide for each of these variables whether you want a value that is as big as possible, or as small as possible.
 (d) Fizeau used `L`=8633 m, `f`=12.6 s?1, and `n`=720. Plug in to your equation from part a and extract the speed of light from his data.(answer check available at lightandmatter.com)

18. (a) Let `R`be the radius of the Earth and `T` the time (one day) that it takes for one rotation. Find the speed at which a point on the equator moves due to the rotation of the earth.(answer check available at lightandmatter.com)
 (b) Check the units of your equation using the method shown in example 1 on p. 27.
 (c) Check that your answer to part a makes sense in the case where the Earth stops rotating completely, so that `T`is infinitely long.
 (d) Nairobi, Kenya, is very close to the equator. Plugging in numbers to your answer from part a, find Nairobi's speed in meters per second. See the table in the back of the book for the relevant data. For comparison, the speed of sound is about 340 m/s.(answer check available at lightandmatter.com)

19. (a) Let `theta`be the latitude of a point on the Earth's surface. Derive an algebra equation for the distance, `L`, traveled by that point during one rotation of the Earth about its axis, i.e., over one day, expressed in terms of `theta` and `R`, the radius of the earth. You may find it helpful to draw one or more diagrams in the style of figure h on p. 34.(answer check available at lightandmatter.com)
 (b) Generalize the result of problem 18a to points not necessarily on the equator.(answer check available at lightandmatter.com)
 (c) Check the units of your equation using the method shown in example 1 on p. 27.
 (d) Check that your equation in part b gives zero for the North Pole, and also that it agrees with problem 18a in the special case of a point on the equator.
 (e) At what speed is Fullerton, California, at latitude `theta`=34°, moving with the rotation of the Earth about its axis?(answer check available at lightandmatter.com)