8.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
The velocity vector points in the direction of the object's motion. Relative motion can be described by vector addition of velocities.
The acceleration vector need not point in the same direction as the object's motion. We use the word “acceleration” to describe any change in an object's velocity vector, which can be either a change in its magnitude or a change in its direction.
An important application of the vector addition of forces is the use of Newton's first law to analyze mechanical systems.
Problems
Key
`srqt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
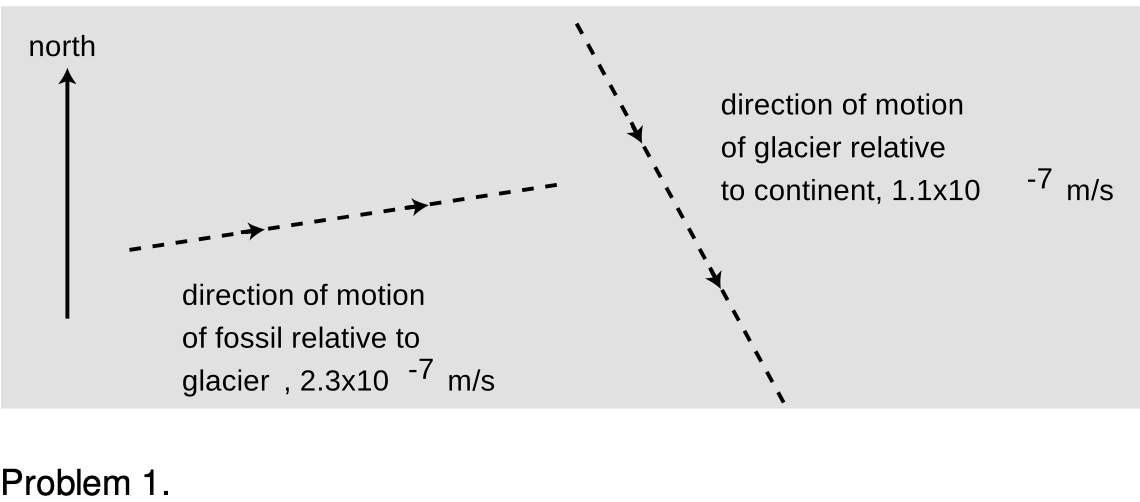 1. A dinosaur fossil is slowly moving down the slope of a glacier under the influence of wind, rain and gravity. At the same time, the glacier is moving relative to the continent underneath. The dashed lines represent the directions but not the magnitudes of the velocities. Pick a scale, and use graphical addition of vectors to find the magnitude and the direction of the fossil's velocity relative to the continent. You will need a ruler and protractor.
1. A dinosaur fossil is slowly moving down the slope of a glacier under the influence of wind, rain and gravity. At the same time, the glacier is moving relative to the continent underneath. The dashed lines represent the directions but not the magnitudes of the velocities. Pick a scale, and use graphical addition of vectors to find the magnitude and the direction of the fossil's velocity relative to the continent. You will need a ruler and protractor.
2. Is it possible for a helicopter to have an acceleration due east and a velocity due west? If so, what would be going on? If not, why not?
3. A bird is initially flying horizontally east at 21.1 m/s, but one second later it has changed direction so that it is flying horizontally and `7°` north of east, at the same speed. What are the magnitude and direction of its acceleration vector during that one second time interval? (Assume its acceleration was roughly constant.)
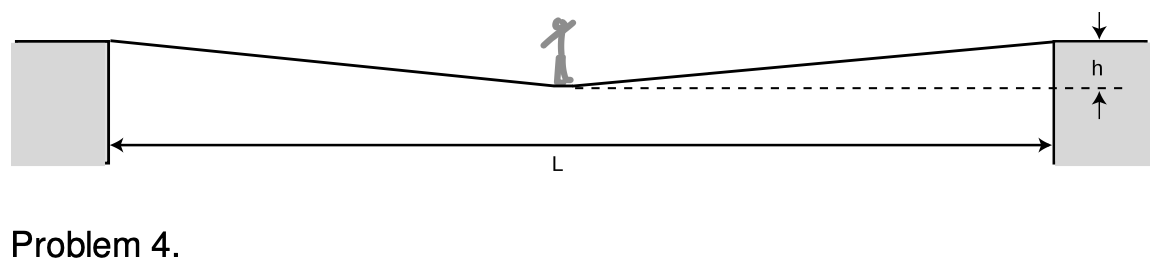 4. A person of mass `M` stands in the middle of a tightrope, which is fixed at the ends to two buildings separated by a horizontal distance `L`. The rope sags in the middle, stretching and lengthening the rope slightly.
4. A person of mass `M` stands in the middle of a tightrope, which is fixed at the ends to two buildings separated by a horizontal distance `L`. The rope sags in the middle, stretching and lengthening the rope slightly.
(a) If the tightrope walker wants the rope to sag vertically by no more than a height `h`, find the minimum tension, `T`, that the rope must be able to withstand without breaking, in terms of `h`, `g`, `M`, and `L`.
(b) Based on your equation, explain why it is not possible to get `h=0`, and give a physical interpretation.
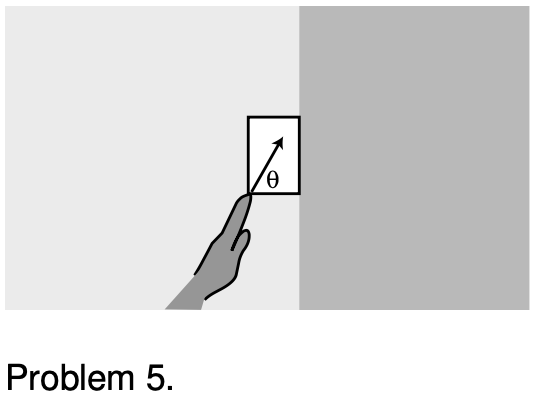 5. Your hand presses a block of mass `m` against a wall with a force `F_H` acting at an angle `theta`, as shown in the figure. Find the minimum and maximum possible values of `|F_H|` that can keep the block stationary, in terms of `m`, `g`, `theta`, and `mus`, the coefficient of static friction between the block and the wall. Check both your answers in the case of `theta=90°`, and interpret the case where the maximum force is infinite.
5. Your hand presses a block of mass `m` against a wall with a force `F_H` acting at an angle `theta`, as shown in the figure. Find the minimum and maximum possible values of `|F_H|` that can keep the block stationary, in terms of `m`, `g`, `theta`, and `mus`, the coefficient of static friction between the block and the wall. Check both your answers in the case of `theta=90°`, and interpret the case where the maximum force is infinite.
6. A skier of mass `m` is coasting down a slope inclined at an angle `theta` compared to horizontal. Assume for simplicity that the treatment of kinetic friction given in chapter 5 is appropriate here, although a soft and wet surface actually behaves a little differently. The coefficient of kinetic friction acting between the skis and the snow is `muk`, and in addition the skier experiences an air friction force of magnitude `bv_2`, where `b` is a constant.
(a) Find the maximum speed that the skier will attain, in terms of the variables `m`, `g`, `theta`, `muk`, and`b`.
(b) For angles below a certain minimum angle `theta_(min)`, the equation gives a result that is not mathematically meaningful. Find an equation for `theta_(min)`, and give a physical explanation of what is happening for `theta<theta_(min)`.
7. A gun is aimed horizontally to the west. The gun is fired, and the bullet leaves the muzzle at `t=0`. The bullet's position vector as a function of time is `r=bhatx+cthaty+dt^2hatz`, where `b`, `c`, and `d` are positive constants.
(a) What units would `b`, `c`, and `d` need to have for the equation to make sense?
(b) Find the bullet's velocity and acceleration as functions of time.
(c) Give physical interpretations of `b`, `c`, `d`, `hatx`, `haty`, and`hatz`?
8. (solution in the pdf version of the book) Annie Oakley, riding north on horseback at 30 mi/hr, shoots her rifle, aiming horizontally and to the northeast. The muzzle speed of the rifle is 140 mi/hr. When the bullet hits a defenseless fuzzy animal, what is its speed of impact? Neglect air resistance, and ignore the vertical motion of the bullet.
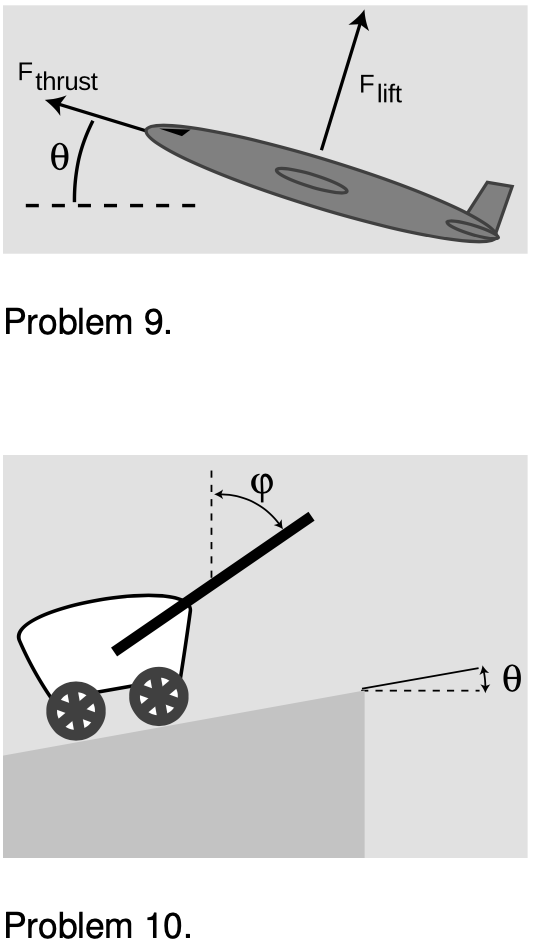 9. (solution in the pdf version of the book) A cargo plane has taken off from a tiny airstrip in the Andes, and is climbing at constant speed, at an angle of `theta`=17° with respect to horizontal. Its engines supply a thrust of `F_"thrust"=200 kN`, and the lift from its wings is `F_"lift"=654 kN`. Assume that air resistance (drag) is negligible, so the only forces acting are thrust, lift, and weight. What is its mass, in kg?
9. (solution in the pdf version of the book) A cargo plane has taken off from a tiny airstrip in the Andes, and is climbing at constant speed, at an angle of `theta`=17° with respect to horizontal. Its engines supply a thrust of `F_"thrust"=200 kN`, and the lift from its wings is `F_"lift"=654 kN`. Assume that air resistance (drag) is negligible, so the only forces acting are thrust, lift, and weight. What is its mass, in kg?
10. A wagon is being pulled at constant speed up a slope `theta` by a rope that makes an angle `phi` with the vertical.
(a) Assuming negligible friction, show that the tension in the rope is given by the equation
`F_T=(sintheta)/(sin(theta+phi))F_W,`
where `F_W` is the weight force acting on the wagon.
(b) Interpret this equation in the special cases of `phi=0` and `phi=180°?theta`.(solution in the pdf version of the book)
11. The angle of repose is the maximum slope on which an object will not slide. On airless, geologically inert bodies like the moon or an asteroid, the only thing that determines whether dust or rubble will stay on a slope is whether the slope is less steep than the angle of repose. (See figure n, p. 266.)
(a) Find an equation for the angle of repose, deciding for yourself what are the relevant variables.
(b) On an asteroid, where `g` can be thousands of times lower than on Earth, would rubble be able to lie at a steeper angle of repose?(solution in the pdf version of the book)
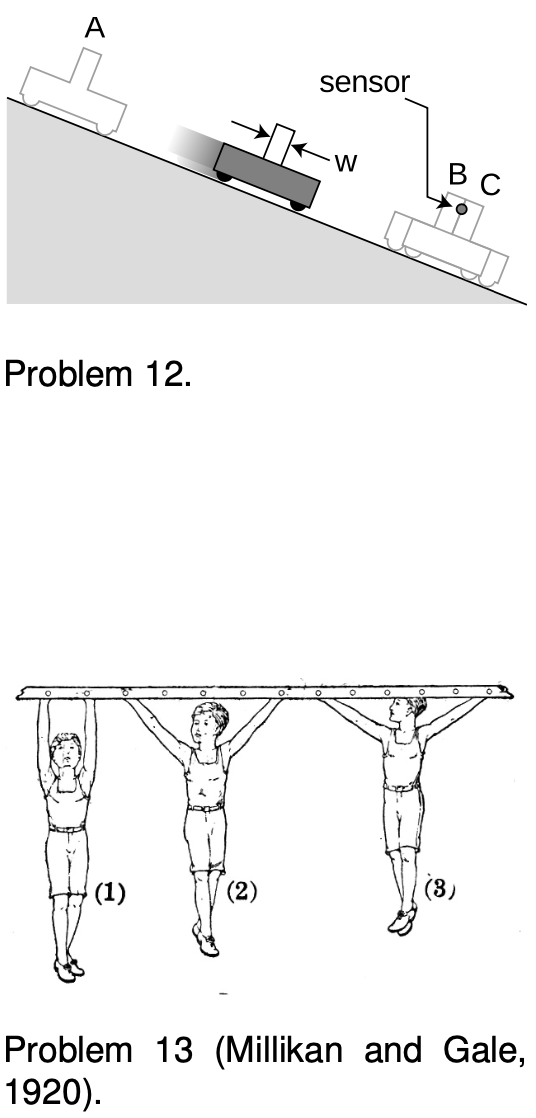 12. The figure shows an experiment in which a cart is released from rest at A, and accelerates down the slope through a distance `x` until it passes through a sensor's light beam. The point of the experiment is to determine the cart's acceleration. At B, a cardboard vane mounted on the cart enters the light beam, blocking the light beam, and starts an electronic timer running. At C, the vane emerges from the beam, and the timer stops.
12. The figure shows an experiment in which a cart is released from rest at A, and accelerates down the slope through a distance `x` until it passes through a sensor's light beam. The point of the experiment is to determine the cart's acceleration. At B, a cardboard vane mounted on the cart enters the light beam, blocking the light beam, and starts an electronic timer running. At C, the vane emerges from the beam, and the timer stops.
(a) Find the final velocity of the cart in terms of the width `w` of the vane and the time `t_b` for which the sensor's light beam was blocked.
(b) Find the magnitude of the cart's acceleration in terms of the measurable quantities `x`, `t_b`, and `w`.
(c) Analyze the forces in which the cart participates, using a table in the format introduced in section 5.3. Assume friction is negligible.
(d) Find a theoretical value for the acceleration of the cart, which could be compared with the experimentally observed value extracted in part `b`. Express the theoretical value in terms of the angle `theta` of the slope, and the strength `g` of the gravitational field.
13. The figure shows a boy hanging in three positions: (1) with his arms straight up, (2) with his arms at 45 degrees, and (3) with his arms at 60 degrees with respect to the vertical. Compare the tension in his arms in the three cases.
14. Driving down a hill inclined at an angle `theta` with respect to horizontal, you slam on the brakes to keep from hitting a deer. Your antilock brakes kick in, and you don't skid.
(a) Analyze the forces. (Ignore rolling resistance and air friction.)
(b) Find the car's maximum possible deceleration, `a` (expressed as a positive number), in terms of `g`, `theta`, and the relevant coefficient of friction.
(c) Explain physically why the car's mass has no effect on your answer.
(d) Discuss the mathematical behavior and physical interpretation of your result for negative values of `theta`.
(e) Do the same for very large positive values of `theta`.
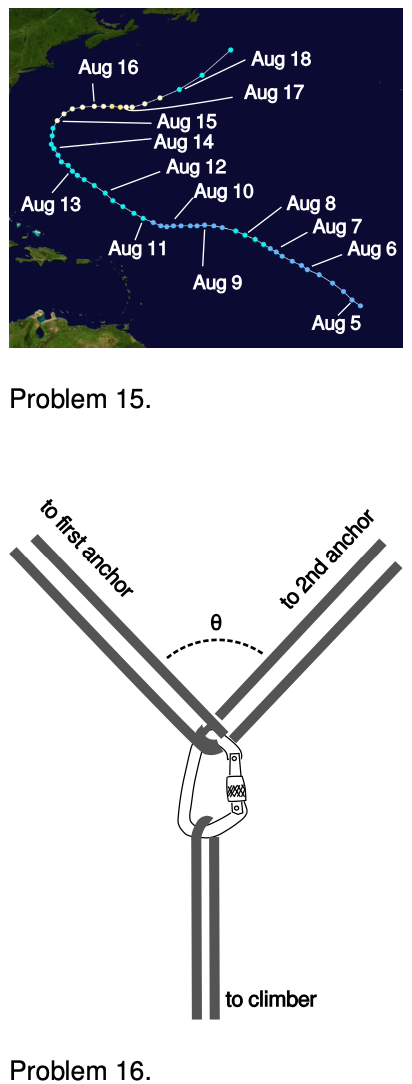 15. The figure shows the path followed by Hurricane Irene in 2005 as it moved north. The dots show the location of the center of the storm at six-hour intervals, with lighter dots at the time when the storm reached its greatest intensity. Find the time when the storm's center had a velocity vector to the northeast and an acceleration vector to the southeast. Explain.
15. The figure shows the path followed by Hurricane Irene in 2005 as it moved north. The dots show the location of the center of the storm at six-hour intervals, with lighter dots at the time when the storm reached its greatest intensity. Find the time when the storm's center had a velocity vector to the northeast and an acceleration vector to the southeast. Explain.
16. For safety, mountain climbers often wear a climbing harness and tie in to other climbers on a rope team or to anchors such as pitons or snow anchors. When using anchors, the climber usually wants to tie in to more than one, both for extra strength and for redundancy in case one fails. The figure shows such an arrangement, with the climber hanging from a pair of anchors forming a “Y” at an angle `theta`. The usual advice is to make `theta<90°`; for large values of `theta`, the stress placed on the anchors can be many times greater than the actual load `L`, so that two anchors are actually less safe than one.
(a) Find the force `S` at each anchor in terms of `L` and `theta`.
(b) Verify that your answer makes sense in the case of `theta=0`.
(c) Interpret your answer in the case of `theta=180°`.
(d) What is the smallest value of `theta` for which `S` equals or exceeds `L`, so that for larger angles a failure of at least one anchor is more likely than it would have been with a single anchor?
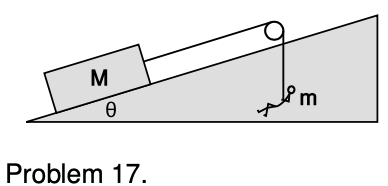 17. (a) The person with mass `m` hangs from the rope, hauling the box of mass `M` up a slope inclined at an angle `theta`. There is friction between the box and the slope, described by the usual coefficients of friction. The pulley, however, is frictionless. Find the magnitude of the box's acceleration.
17. (a) The person with mass `m` hangs from the rope, hauling the box of mass `M` up a slope inclined at an angle `theta`. There is friction between the box and the slope, described by the usual coefficients of friction. The pulley, however, is frictionless. Find the magnitude of the box's acceleration.
(b) Show that the units of your answer make sense.
(c) Check the physical behavior of your answer in the special cases of `M=0` and `theta=-90°`.
18. Complete example 6 on p. 224 by expressing the remaining nine `x` and `y` components of the forces in terms of the five magnitudes and the small, positive angle `theta approx 9°` by which the crack overhangs.
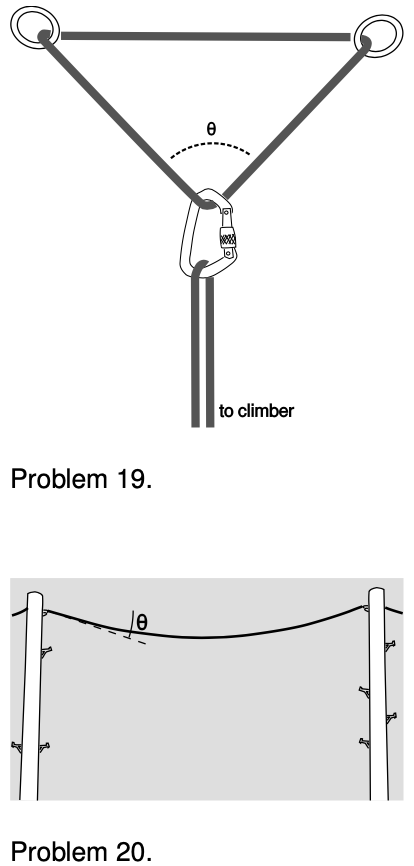 19. Problem 16 discussed a possible correct way of setting up a redundant anchor for mountaineering. The figure for this problem shows an incorrect way of doing it, by arranging the rope in a triangle (which we'll take to be isoceles). One of the bad things about the triangular arrangement is that it requires more force from the anchors, making them more likely to fail. (a) Using the same notation as in problem 16, find `S` in terms of `L` and `theta`.
19. Problem 16 discussed a possible correct way of setting up a redundant anchor for mountaineering. The figure for this problem shows an incorrect way of doing it, by arranging the rope in a triangle (which we'll take to be isoceles). One of the bad things about the triangular arrangement is that it requires more force from the anchors, making them more likely to fail. (a) Using the same notation as in problem 16, find `S` in terms of `L` and `theta`.
(b) Verify that your answer makes sense in the case of `theta=0`, and compare with the correct setup.
20. A telephone wire of mass `m` is strung between two poles, making an angle `theta` with the horizontal at each end.
(a) Find the tension at the center.
(b) Which is greater, the tension at the center or at the ends?
Exercise 8: Vectors and motion
Each diagram on page 237 shows the motion of an object in an `x-y` plane. Each dot is one location of the object at one moment in time. The time interval from one dot to the next is always the same, so you can think of the vector that connects one dot to the next as a `v` vector, and subtract to find `Deltav` vectors.
1. Suppose the object in diagram 1 is moving from the top left to the bottom right. Deduce whatever you can about the force acting on it. Does the force always have the same magnitude? The same direction?
Invent a physical situation that this diagram could represent.
What if you reinterpret the diagram by reversing the object's direction of motion? Redo the construction of one of the `Deltav` vectors and see what happens.
2. What can you deduce about the force that is acting in diagram 2?
Invent a physical situation that diagram 2 could represent.
3. What can you deduce about the force that is acting in diagram 3?
Invent a physical situation.

8.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.