8.2 The acceleration vector by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
8.2 The acceleration vector
When all three acceleration components are constant, i.e., when the `v_x-t`, `v_y-t`, and `v_z-t` graphs are all linear, we can define the acceleration vector as
`a = (Deltav)/(Deltat)` , [Only for constant acceleration]
which can be written in terms of initial and final velocities as
`a=(v_f - v_i)/(Deltat) `. [Only for constant acceleration]
 If the acceleration is not constant, we define it as the vector made out of the `a_x`, `a_y`, and `a_z` components found by applying the slope-of-the-tangent-line technique to the `v_x-t`, `v_y-t`, and `v_z-t` graphs.
If the acceleration is not constant, we define it as the vector made out of the `a_x`, `a_y`, and `a_z` components found by applying the slope-of-the-tangent-line technique to the `v_x-t`, `v_y-t`, and `v_z-t` graphs.
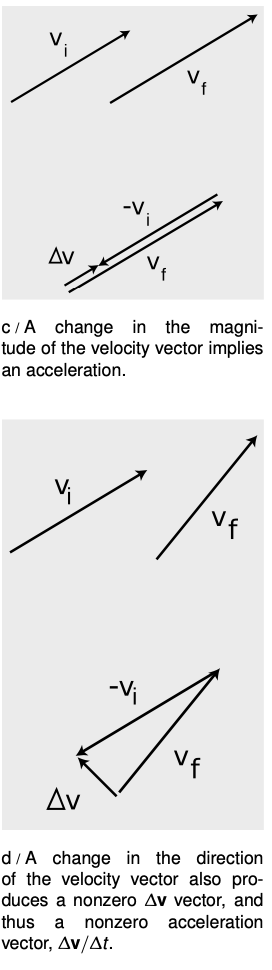
Now there are two ways in which we could have a nonzero acceleration. Either the magnitude or the direction of the velocity vector could change. This can be visualized with arrow diagrams as shown in figures c and d. Both the magnitude and direction can change simultaneously, as when a car accelerates while turning. Only when the magnitude of the velocity changes while its direction stays constant do we have a `Deltav` vector and an acceleration vector along the same line as the motion.
self-check:
(1) In figure c, is the object speeding up, or slowing down? (2) What would the diagram look like if `v_i` was the same as `v_f`? (3) Describe how the `Deltav` vector is different depending on whether an object is speeding up or slowing down.
(answer in the back of the PDF version of the book)
If this all seems a little strange and abstract to you, you're not alone. It doesn't mean much to most physics students the first time someone tells them that acceleration is a vector, and that the acceleration vector does not have to be in the same direction as the velocity vector. One way to understand those statements better is to imagine an object such as an air freshener or a pair of fuzzy dice hanging from the rear-view mirror of a car. Such a hanging object, called a bob, constitutes an accelerometer. If you watch the bob as you accelerate from a stop light, you'll see it swing backward. The horizontal direction in which the bob tilts is opposite to the direction of the acceleration. If you apply the brakes and the car's acceleration vector points backward, the bob tilts forward.
After accelerating and slowing down a few times, you think you've put your accelerometer through its paces, but then you make a right turn. Surprise! Acceleration is a vector, and needn't point in the same direction as the velocity vector. As you make a right turn, the bob swings outward, to your left. That means the car's acceleration vector is to your right, perpendicular to your velocity vector. A useful definition of an acceleration vector should relate in a systematic way to the actual physical effects produced by the acceleration, so a physically reasonable definition of the acceleration vector must allow for cases where it is not in the same direction as the motion.
self-check:
In projectile motion, what direction does the acceleration vector have?
(answer in the back of the PDF version of the book)
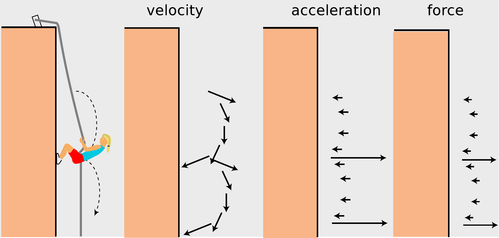
Example 2: Rappelling
In figure e, the rappeller's velocity has long periods of gradual change interspersed with short periods of rapid change. These correspond to periods of small acceleration and force, and periods of large acceleration and force.
f / Example 3.
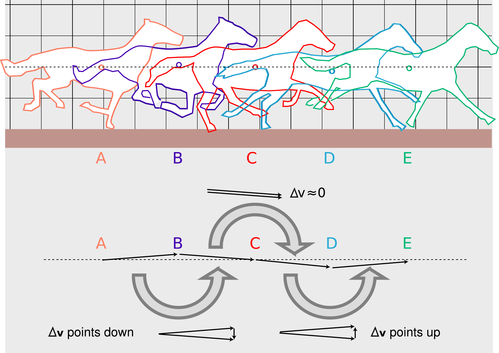
Example 3: The galloping horse
Figure f on page 222 shows outlines traced from the first, third, fifth, seventh, and ninth frames in Muybridge's series of photographs of the galloping horse. The estimated location of the horse's center of mass is shown with a circle, which bobs above and below the horizontal dashed line.
If we don't care about calculating velocities and accelerations in any particular system of units, then we can pretend that the time between frames is one unit. The horse's velocity vector as it moves from one point to the next can then be found simply by drawing an arrow to connect one position of the center of mass to the next. This produces a series of velocity vectors which alternate between pointing above and below horizontal.
The `Deltav` vector is the vector which we would have to add onto one velocity vector in order to get the next velocity vector in the series. The `Deltav` vector alternates between pointing down (around the time when the horse is in the air, B) and up (around the time when the horse has two feet on the ground, D).
Discussion Questions
`mathbf"A"` When a car accelerates, why does a bob hanging from the rearview mirror swing toward the back of the car? Is it because a force throws it backward? If so, what force? Similarly, describe what happens in the other cases described above.
`mathbf"B"` Superman is guiding a crippled spaceship into port. The ship's engines are not working. If Superman suddenly changes the direction of his force on the ship, does the ship's velocity vector change suddenly? Its acceleration vector? Its direction of motion?
8.2 The acceleration vector by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.