7.3 Techniques for adding vectors by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
7.3 Techniques for adding vectors
Vector addition is one of the three essential mathematical skills, summarized on pp.532-533, that you need for success in this course.
Addition of vectors given their components
The easiest type of vector addition is when you are in possession of the components, and want to find the components of their sum.
Example 6: Adding components
`=>` Given the `Deltax` and `Deltay` values from the previous examples, find the `Deltax` and `Deltay` from San Diego to Las Vegas.
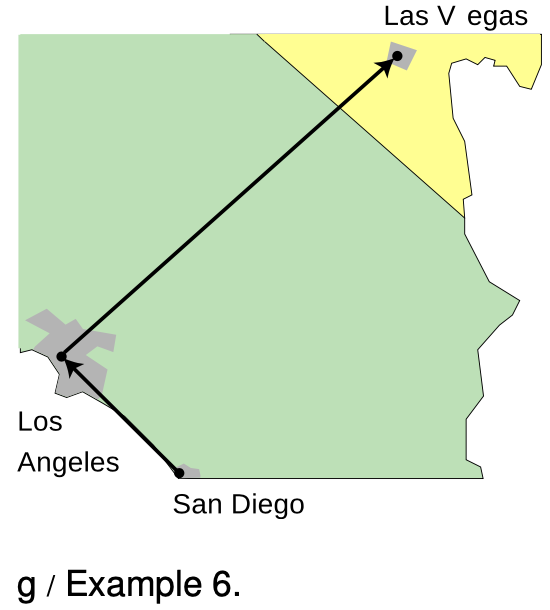 `=>`
`=>`
` =-120 km+290 km`
`=170 km`
`=150 km+230 km`
`=380`
Note how the signs of the `x` components take care of the westward and eastward motions, which partially cancel.
Addition of vectors given their magnitudes and directions
In this case, you must first translate the magnitudes and directions into 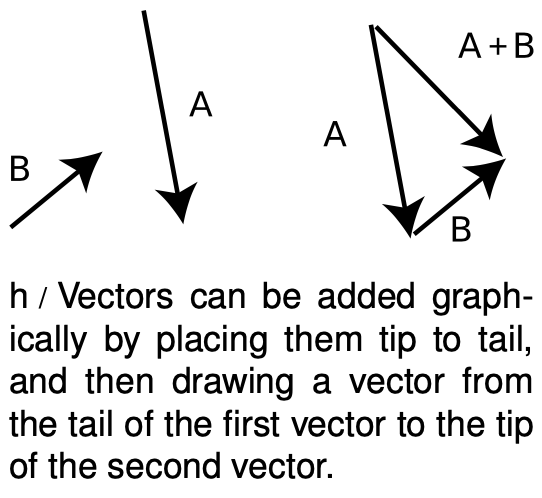 components, and the add the components. In our San Diego-Los Angeles-Las Vegas example, we can simply string together the preceding examples; this is done on p. 533.
components, and the add the components. In our San Diego-Los Angeles-Las Vegas example, we can simply string together the preceding examples; this is done on p. 533.
Graphical addition of vectors
Often the easiest way to add vectors is by making a scale drawing on a piece of paper. This is known as graphical addition, as opposed to the analytic techniques discussed previously. (It has nothing to do with `x-y` graphs or graph paper. “Graphical” here simply means drawing. It comes from the Greek verb “grapho,” to write, like related English words including “graphic.”)
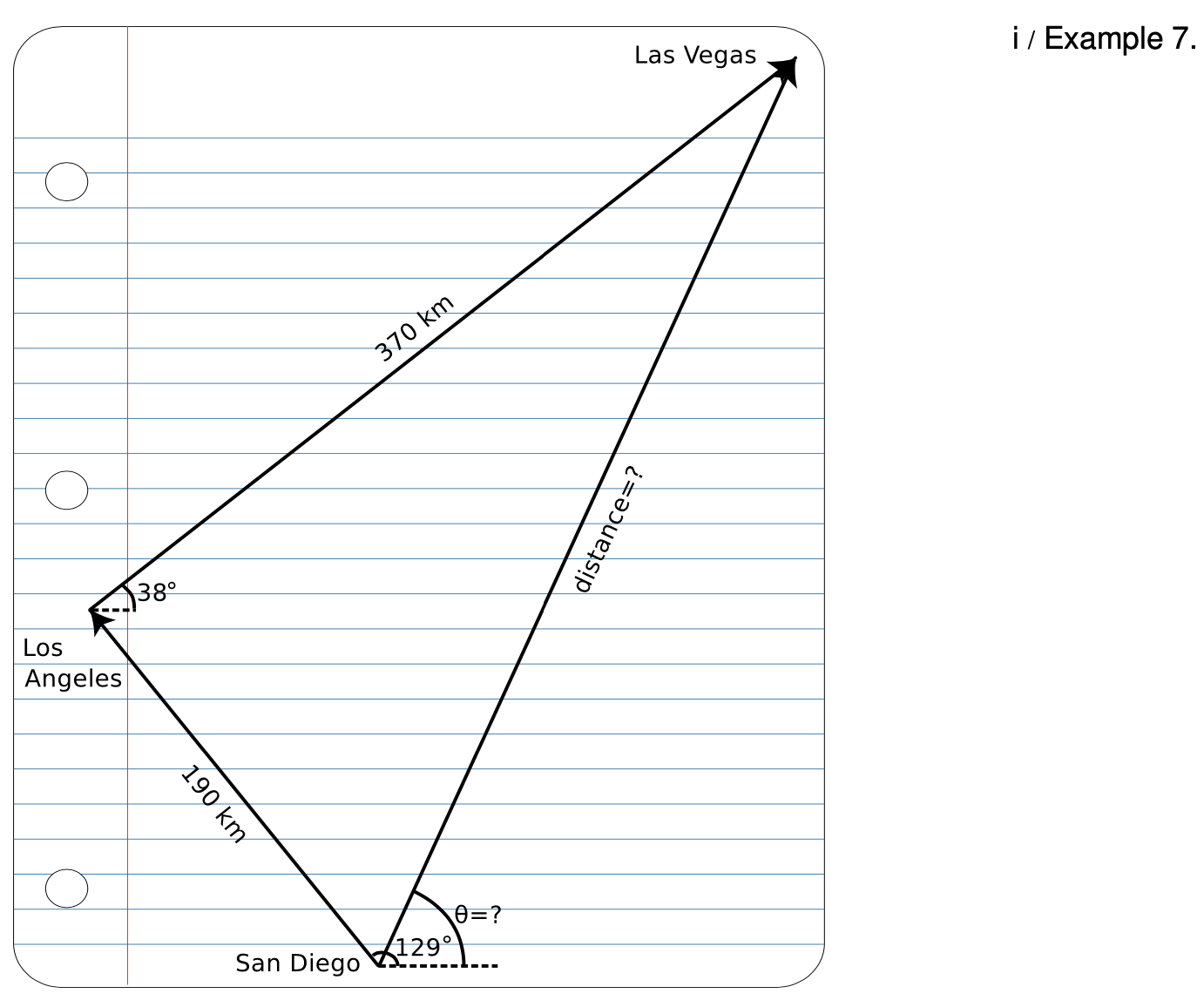
Example 7: LA to Vegas, graphically
`=>` Given the magnitudes and angles of the `Deltar` vectors from San Diego to Los Angeles and from Los Angeles to Las Vegas, find the magnitude and angle of the `Deltar` vector from San Diego to Las Vegas.
`=>` Using a protractor and a ruler, we make a careful scale drawing, as shown in figure i. The protractor can be conveniently aligned with the blue rules on the notebook paper. A scale of `1 mm->2 km` was chosen for this solution because it was as big as possible (for accuracy) without being so big that the drawing wouldn't fit on the page. With a ruler, we measure the distance from San Diego to Las Vegas to be 206 mm, which corresponds to 412 km. With a protractor, we measure the angle `theta` to be 65°.
 Even when we don't intend to do an actual graphical calculation with a ruler and protractor, it can be convenient to diagram the addition of vectors in this way. With `Deltar` vectors, it intuitively makes sense to lay the vectors tip-to-tail and draw the sum vector from the tail of the first vector to the tip of the second vector. We can do the same when adding other vectors such as force vectors.
Even when we don't intend to do an actual graphical calculation with a ruler and protractor, it can be convenient to diagram the addition of vectors in this way. With `Deltar` vectors, it intuitively makes sense to lay the vectors tip-to-tail and draw the sum vector from the tail of the first vector to the tip of the second vector. We can do the same when adding other vectors such as force vectors.
self-check:
How would you subtract vectors graphically?
(answer in the back of the PDF version of the book)
Discussion Questions
`mathbf"A"` If you're doing graphical addition of vectors, does it matter which vector you start with and which vector you start from the other vector's tip?
`mathbf"B"` If you add a vector with magnitude 1 to a vector of magnitude 2, what magnitudes are possible for the vector sum?
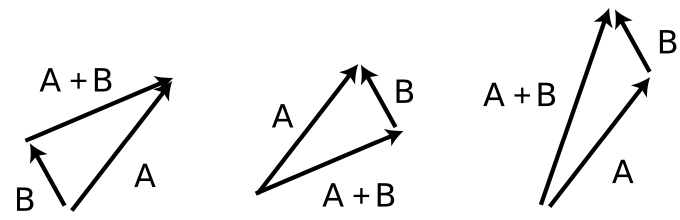
`mathbf"C"` Which of these examples of vector addition are correct, and which are incorrect?
7.3 Techniques for adding vectors by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.