7.2 Calculations with magnitude and direction by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
7.2 Calculations with magnitude and direction
If you ask someone where Las Vegas is compared to Los Angeles, they are unlikely to say that the `Deltax` is 290 km and the `Deltay` is 230 km, in a coordinate system where the positive `x` axis is east and the `y` axis points north. They will probably say instead that it's 370 km to the northeast. If they were being precise, they might give the direction as `38°` counterclockwise from east. In two dimensions, we can always specify a vector's direction like this, using a single angle. A magnitude plus an angle suffice to specify everything about the vector. The following two examples show how we use trigonometry and the Pythagorean theorem to go back and forth between the `x-y` and magnitude-angle descriptions of vectors.
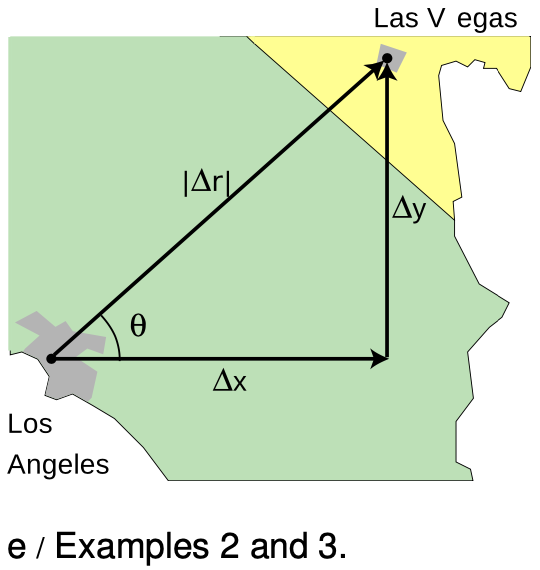 Example 2: Finding magnitude and angle from components
Example 2: Finding magnitude and angle from components
`=>` Given that the `Deltar` vector from LA to Las Vegas has `Deltax=290 km` and `Deltay=230 km`, how would we find the magnitude and direction of `Deltar`?
`=>` We find the magnitude of `Deltar` from the Pythagorean theorem:
`=370 km`
We know all three sides of the triangle, so the angle `theta` can be found using any of the inverse trig functions. For example, we know the opposite and adjacent sides, so
`theta = tan^(-1)((Deltay)/(Deltax))`
` =38°`.
Example 3: Finding components from magnitude and angle
`=>` Given that the straight-line distance from Los Angeles to Las Vegas is 370 km, and that the angle `theta` in the figure is 38°, how can the `x` and `y` components of the `Deltar` vector be found?
`=>` The sine and cosine of `theta` relate the given information to the information we wish to find:
`cos theta = (deltax)/|Deltar|`
`sin theta = (deltay)/|Deltar|`
Solving for the unknowns gives
`Delta x = |Deltar|*cos theta`
`=290 kmand`
`Delta y = |Deltar|*sin theta`
`=230 km.`
The following example shows the correct handling of the plus and minus signs, which is usually the main cause of mistakes.
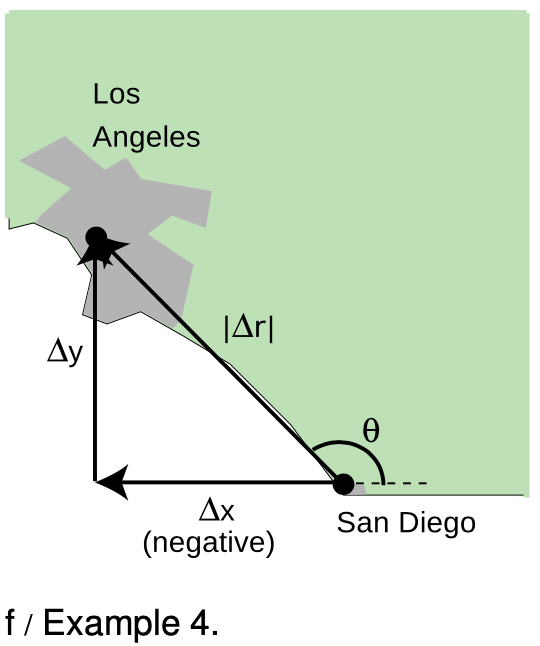 Example 4: Negative components
Example 4: Negative components
`=>` San Diego is 120 km east and 150 km south of Los Angeles. An airplane pilot is setting course from San Diego to Los Angeles. At what angle should she set her course, measured counterclockwise from east, as shown in the figure?
`=>` If we make the traditional choice of coordinate axes, with `x` pointing to the right and `y` pointing up on the map, then her `Deltax` is negative, because her final `x` value is less than her initial `x` value. Her `Deltay` is positive, so we have
`Deltax=-120 km`
`Deltay=150 km.`
If we work by analogy with example 2, we get
`theta = tan^(-1)((Deltay)/(Deltax))`
`=tan^(-1)(-1.25)`
`=-51°.`
According to the usual way of defining angles in trigonometry, a negative result means an angle that lies clockwise from the x axis, which would have her heading for the Baja California. What went wrong? The answer is that when you ask your calculator to take the arctangent of a number, there are always two valid possibilities differing by 180°. That is, there are two possible angles whose tangents equal -1.25:
`tan129°=-1.25`
`tan-51°=-1.25`
You calculator doesn't know which is the correct one, so it just picks one. In this case, the one it picked was the wrong one, and it was up to you to add 180° to it to find the right answer.
Example 5: A shortcut
`=>` A split second after nine o'clock, the hour hand on a clock dial has moved clockwise past the nine-o'clock position by some imperceptibly small angle `phi`. Let positive `x` be to the right and positive `y` up. If the hand, with length `ℓ`, is represented by a `Deltar` vector going from the dial's center to the tip of the hand, find this vector's `Deltax`.
`=>` The following shortcut is the easiest way to work out examples like these, in which a vector's direction is known relative to one of the axes. We can tell that `Deltar` will have a large, negative `x` component and a small, positive `y`. Since `Deltax`<0, there are really only two logical possibilities: either `Deltax=-ℓcosphi`, or `Deltax=-ℓsinphi`. Because `phi` is small, `cosphi` is large and `sinphi` is small. We conclude that `Deltax=-ℓcosphi`.
A typical application of this technique to force vectors is given in example 6 on p. 224.
Discussion Question
`mathbf"A"` In example 4, we dealt with components that were negative. Does it make sense to classify vectors as positive and negative?
7.2 Calculations with magnitude and direction by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.