7.1 Vector notation by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
7.1 Vector notation
The idea of components freed us from the confines of one-dimensional physics, but the component notation can be unwieldy, since every one-dimensional equation has to be written as a set of three separate equations in the three-dimensional case. Newton was stuck with the component notation until the day he died, but eventually someone sufficiently lazy and clever figured out a way of abbreviating three equations as one.
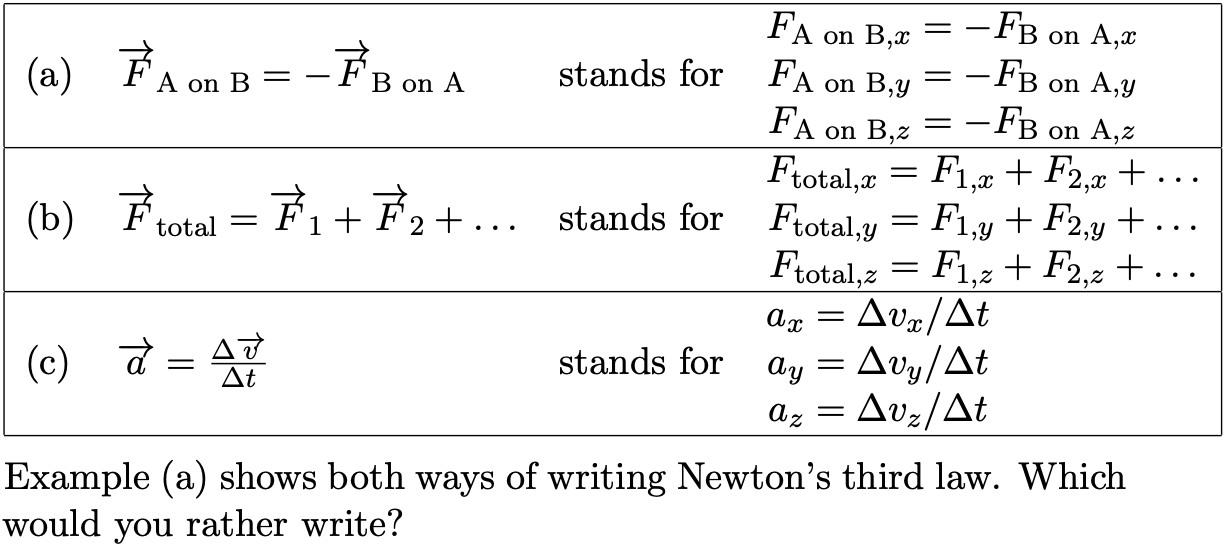
Example (a) shows both ways of writing Newton's third law. Which would you rather write?
The idea is that each of the algebra symbols with an arrow written on top, called a vector, is actually an abbreviation for three different numbers, the `x`, `y`, and `z` components. The three components are referred to as the components of the vector, e.g.,`F_x` is the `x` component of the vector `F?`. The notation with an arrow on top is good for handwritten equations, but is unattractive in a printed book, so books use boldface, `F`, to represent vectors. After this point, I'll use boldface for vectors throughout this book.
Quantities can be classified as vectors or scalars. In a phrase like “a ___ to the northeast,” it makes sense to fill in the blank with “force” or “velocity,” which are vectors, but not with “mass” or “time,” which are scalars. Any nonzero vector has both a direction and an amount. The amount is called its magnitude. The notation for the magnitude of a vector `A` is |`A`|, like the absolute value sign used with scalars.
Often, as in example (b), we wish to use the vector notation to represent adding up all the `x` components to get a total `x` component, etc. The plus sign is used between two vectors to indicate this type of component-by-component addition. Of course, vectors are really triplets of numbers, not numbers, so this is not the same as the use of the plus sign with individual numbers. But since we don't want to have to invent new words and symbols for this operation on vectors, we use the same old plus sign, and the same old addition-related words like “add,” “sum,” and “total.” Combining vectors this way is called vector addition.
Similarly, the minus sign in example (a) was used to indicate negating each of the vector's three components individually. The equals sign is used to mean that all three components of the vector on the left side of an equation are the same as the corresponding components on the right.
Example (c) shows how we abuse the division symbol in a similar manner. When we write the vector `Deltav` divided by the scalar `Deltat`, we mean the new vector formed by dividing each one of the velocity components by `Deltat`.
It's not hard to imagine a variety of operations that would combine vectors with vectors or vectors with scalars, but only four of them are required in order to express Newton's laws:

As an example of an operation that is not useful for physics, there just aren't any useful physics applications for dividing a vector by another vector component by component. In optional section 7.5, we discuss in more detail the fundamental reasons why some vector operations are useful and others useless.
We can do algebra with vectors, or with a mixture of vectors and scalars in the same equation. Basically all the normal rules of algebra apply, but if you're not sure if a certain step is valid, you should simply translate it into three component-based equations and see if it works.
Example 1: Order of addition
`=>` If we are adding two force vectors, `F+G`, is it valid to assume as in ordinary algebra that `F+G` is the same as `G+F`?
`=>` To tell if this algebra rule also applies to vectors, we simply translate the vector notation into ordinary algebra notation. In terms of ordinary numbers, the components of the vector `F+G` would be `F_x+G_x`, `F_y+G_y`, and `F_z+G_z`, which are certainly the same three numbers as `G_x+F_x`, `G_y+F_y`, and `G_z+F_z`. Yes, `F+G` is the same as `G+F`.
It is useful to define a symbol `r` for the vector whose components are `x`, `y`, and `z`, and a symbol `Deltar` made out of `Deltax`, `Deltay`, and `Deltaz`.
Although this may all seem a little formidable, keep in mind that it amounts to nothing more than a way of abbreviating equations! Also, to keep things from getting too confusing the remainder of this chapter focuses mainly on the `Deltar` vector, which is relatively easy to visualize.
self-check:
Translate the equations `v_x=Deltax"/"Deltat`,`v_y=Deltay"/"Deltat`, and `v_z=Deltaz"/"Deltat` for motion with constant velocity into a single equation in vector notation.
(answer in the back of the PDF version of the book)
Drawing vectors as arrows
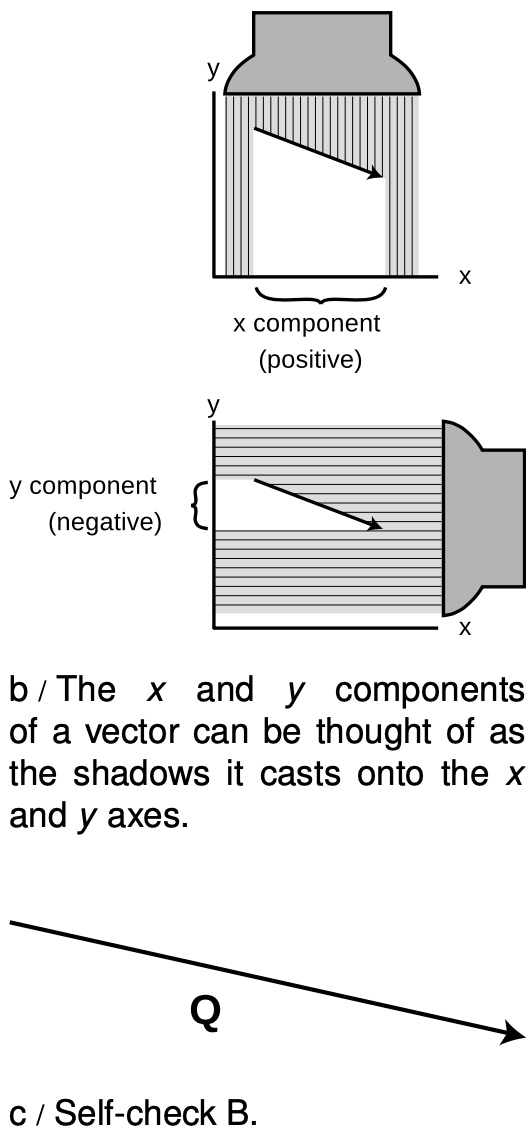 A vector in two dimensions can be easily visualized by drawing an arrow whose length represents its magnitude and whose direction represents its direction. The `x` component of a vector can then be visualized as the length of the shadow it would cast in a beam of light projected onto the `x` axis, and similarly for the `y` component. Shadows with arrowheads pointing back against the direction of the positive axis correspond to negative components.
A vector in two dimensions can be easily visualized by drawing an arrow whose length represents its magnitude and whose direction represents its direction. The `x` component of a vector can then be visualized as the length of the shadow it would cast in a beam of light projected onto the `x` axis, and similarly for the `y` component. Shadows with arrowheads pointing back against the direction of the positive axis correspond to negative components.
In this type of diagram, the negative of a vector is the vector with the same magnitude but in the opposite direction. Multiplying a vector by a scalar is represented by lengthening the arrow by that factor, and similarly for division.
self-check B
Given vector `Q` represented by an arrow in figure c, draw arrows representing the vectors `1.5Q` and `-Q`.
(answer in the back of the PDF version of the book)
This leads to a way of defining vectors and scalars that reflects how physicists think in general about these things:
 For example, a force reverses itself under a 180-degree rotation, but a mass doesn't. We could have defined a vector as something that had both a magnitude and a direction, but that would have left out zero vectors, which don't have a direction. A zero vector is a legitimate vector, because it behaves the same way under rotations as a zero-length arrow, which is simply a dot.
For example, a force reverses itself under a 180-degree rotation, but a mass doesn't. We could have defined a vector as something that had both a magnitude and a direction, but that would have left out zero vectors, which don't have a direction. A zero vector is a legitimate vector, because it behaves the same way under rotations as a zero-length arrow, which is simply a dot.
A remark for those who enjoy brain-teasers: not everything is a vector or a scalar. An American football is distorted compared to a sphere, and we can measure the orientation and amount of that distortion quantitatively. The distortion is not a vector, since a 180-degree rotation brings it back to its original state. Something similar happens with playing cards, figure d. For some subatomic particles, such as electrons, 360 degrees isn't even enough; a 720-degree rotation is needed to put them back the way they were!
Discussion Questions
`mathbf"A"` You drive to your friend's house. How does the magnitude of your `Deltar` vector compare with the distance you've added to the car's odometer?
7.1 Vector notation by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
