6.2 Coordinates and components by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
6.2 Coordinates and components
 'Cause we're all
'Cause we're all
Bold as love,
Just ask the axis. -- Jimi Hendrix
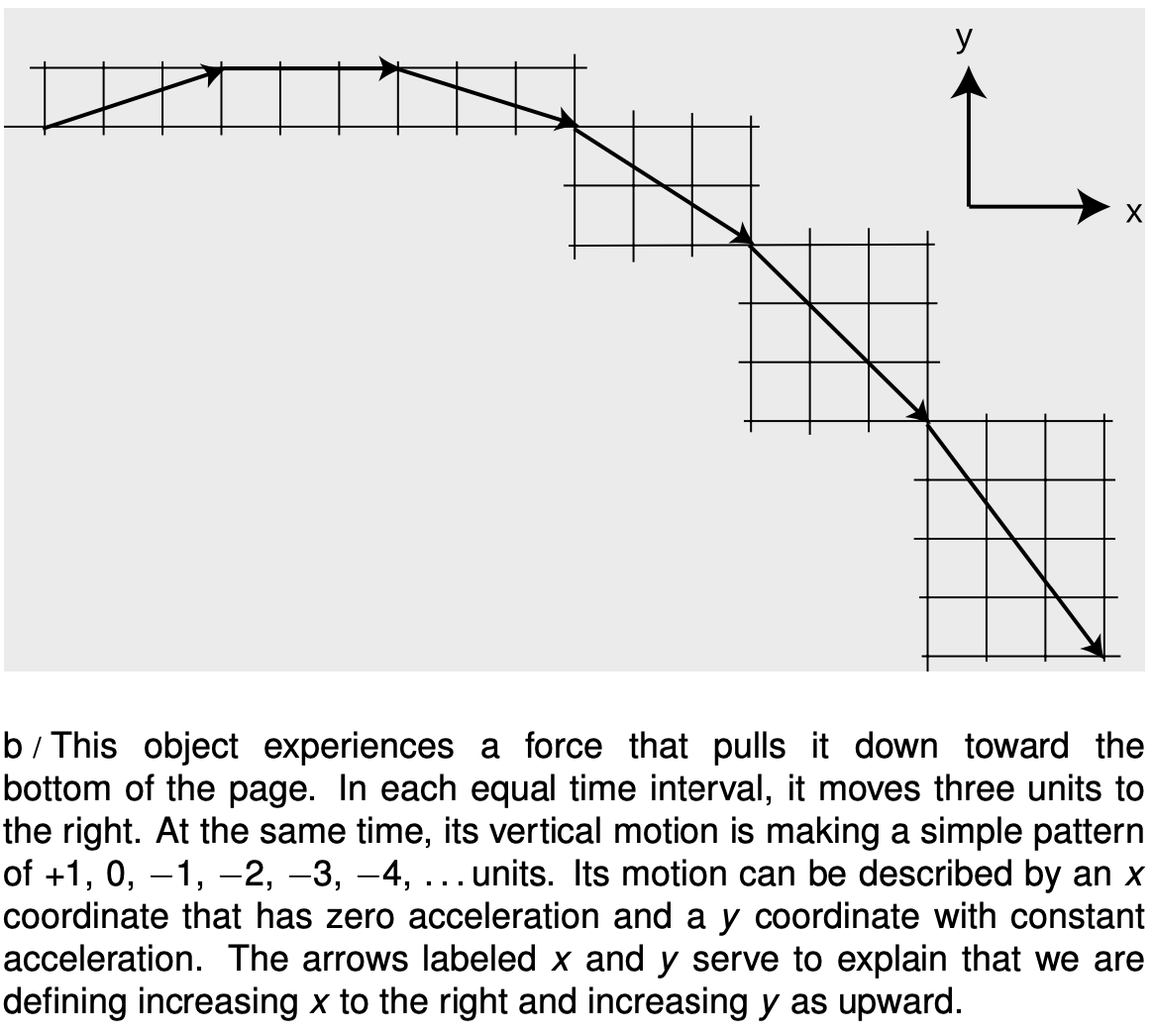
How do we convert these ideas into mathematics? Figure b shows a good way of connecting the intuitive ideas to the numbers. In one dimension, we impose a number line with an `x` coordinate on a certain stretch of space. In two dimensions, we imagine a grid of squares which we label with `x` and `y` values, as shown in figure b.
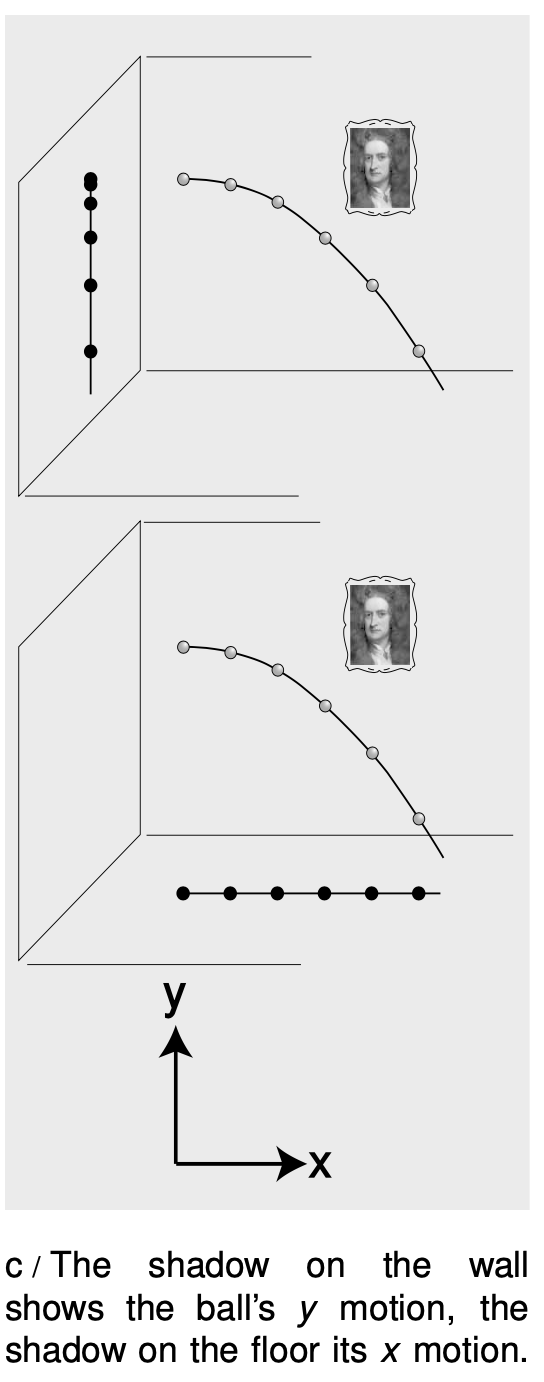
But of course motion doesn't really occur in a series of discrete hops like in chess or checkers. Figure c shows a way of conceptualizing the smooth variation of the `x` and `y` coordinates. The ball's shadow on the wall moves along a line, and we describe its position with a single coordinate, `y`, its height above the floor. The wall shadow has a constant acceleration of -9.8 m/`s^2`. A shadow on the floor, made by a second light source, also moves along a line, and we describe its motion with an `x` coordinate, measured from the wall.
The velocity of the floor shadow is referred to as the `x` component of the velocity, written `v_x`. Similarly we can notate the acceleration of the floor shadow as `a_x`. Since `v_x` is constant, `a_x` is zero.
Similarly, the velocity of the wall shadow is called `v_y`, its acceleration ay. This example has `a_y` = -9.8m/`s^2`.
 Because the earth's gravitational force on the ball is acting along the `y` axis, we say that the force has a negative `y` component, `F_y`, but `F_x=F_z=0`.
Because the earth's gravitational force on the ball is acting along the `y` axis, we say that the force has a negative `y` component, `F_y`, but `F_x=F_z=0`.
The general idea is that we imagine two observers, each of whom perceives the entire universe as if it was flattened down to a single line. The `y`-observer, for instance, perceives `y`, `v_y`, and `a_y`, and will infer that there is a force, `F_y`, acting downward on the ball. That is, a `y` component means the aspect of a physical phenomenon, such as velocity, acceleration, or force, that is observable to someone who can only see motion along the `y` axis.
All of this can easily be generalized to three dimensions. In the example above, there could be a `z`-observer who only sees motion toward or away from the back wall of the room.
`=>` The police find a car at a distance `w=20 m` from the base of a cliff of height `h=100 m`. How fast was the car going when it went over the edge? Solve the problem symbolically first, then plug in the numbers.
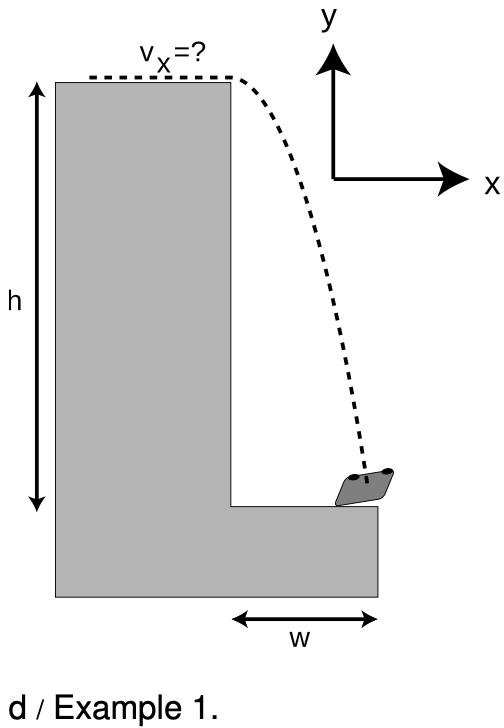 `=>` Let's choose `y` pointing up and `x` pointing away from the cliff. The car's vertical motion was independent of its horizontal motion, so we know it had a constant vertical acceleration of `a=-g=-9.8`m/`s^2`. The time it spent in the air is therefore related to the vertical distance it fell by the constant-acceleration equation
`=>` Let's choose `y` pointing up and `x` pointing away from the cliff. The car's vertical motion was independent of its horizontal motion, so we know it had a constant vertical acceleration of `a=-g=-9.8`m/`s^2`. The time it spent in the air is therefore related to the vertical distance it fell by the constant-acceleration equation
or
Solving for `Deltat` gives
Since the vertical force had no effect on the car's horizontal motion, it had `a_x=0`, i.e., constant horizontal velocity. We can apply the constant-velocity equation
`v_x = Delta x"/"Delta t`,
i.e.,
We now substitute for `Deltat` to find
which simplifies to
Plugging in numbers, we find that the car's speed when it went over the edge was 4 m/s, or about 10 mi/hr.
Projectiles move along parabolas.
 What type of mathematical curve does a projectile follow through space? To find out, we must relate `x` to `y`, eliminating `t`. The reasoning is very similar to that used in the example above. Arbitrarily choosing `x=y=t=0` to be at the top of the arc, we conveniently have `x=Deltax`, `y=Deltay`, and `t=Deltat`, so
What type of mathematical curve does a projectile follow through space? To find out, we must relate `x` to `y`, eliminating `t`. The reasoning is very similar to that used in the example above. Arbitrarily choosing `x=y=t=0` to be at the top of the arc, we conveniently have `x=Deltax`, `y=Deltay`, and `t=Deltat`, so
`y_x=1/2a_yt^2` `(a_y<0)`
`x = v_x t`|
We solve the second equation for`t=x/(v_xt)` and eliminate`t` in the first equation:
Since everything in this equation is a constant except for `x` and `y`, we conclude that `y` is proportional to the square of `x`. As you may or may not recall from a math class, `ypropx^2` describes a parabola.
`=>` Solved problem: A cannon — problem 5
Discussion Question
 `mathbf"A"` At the beginning of this section I represented the motion of a projectile on graph paper, breaking its motion into equal time intervals. Suppose instead that there is no force on the object at all. It obeys Newton's first law and continues without changing its state of motion. What would the corresponding graph-paper diagram look like? If the time interval represented by each arrow was 1 second, how would you relate the graph-paper diagram to the velocity components `v_x` and `v_y`?
`mathbf"A"` At the beginning of this section I represented the motion of a projectile on graph paper, breaking its motion into equal time intervals. Suppose instead that there is no force on the object at all. It obeys Newton's first law and continues without changing its state of motion. What would the corresponding graph-paper diagram look like? If the time interval represented by each arrow was 1 second, how would you relate the graph-paper diagram to the velocity components `v_x` and `v_y`?
`mathbf"B"` Make up several different coordinate systems oriented in different ways, and describe the `a_x` and `a_y` of a falling object in each one.
6.2 Coordinates and components by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
