3.9 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
gravity — A general term for the phenomenon of attraction between things having mass. The attraction between our planet and a human-sized object causes the object to fall.
acceleration — The rate of change of velocity; the slope of the tangent line on a v-t graph.
Notation
`v_o`— initial velocity
`v_f` — final velocity
`a`— acceleration
`g` — the acceleration of objects in free fall; the strength of the local gravitational field
Summary
Galileo showed that when air resistance is negligible all falling bodies have the same motion regardless of mass. Moreover, their `v-t` graphs are straight lines. We therefore define a quantity called acceleration as the slope, `Deltav`/`Deltat`, of an object's v-t graph. In cases other than free fall, the v-t graph may be curved, in which case the definition is generalized as the slope of a tangent line on the v-t graph. The acceleration of objects in free fall varies slightly across the surface of the earth, and greatly on other planets.
Positive and negative signs of acceleration are defined according to whether the v-t graph slopes up or down. This definition has the advantage that a force with a given sign, representing its direction, always produces an acceleration with the same sign.
The area under the v-t graph gives `Deltax`, and analogously the area under the a-t graph gives `Deltav`.
For motion with constant acceleration, the following three equations hold:
`Deltax = v_0 *t + (1"/"2)a *t^2`
`v_f^2 = v_0^2 + 2a*Deltax`
`a = Deltav `/` Deltat`
They are not valid if the acceleration is changing.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
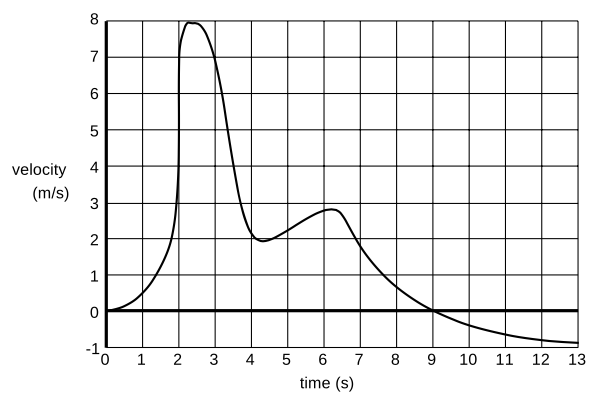
1. The graph represents the velocity of a bee along a straight line. At `t=0`, the bee is at the hive. (a) When is the bee farthest from the hive? (b) How far is the bee at its farthest point from the hive? (c) At `t=13`s, how far is the bee from the hive? [Hint: Try problem 19 first.] `sqrt`
2. A rock is dropped into a pond. Draw plots of its position versus time, velocity versus time, and acceleration versus time. Include its whole motion, starting from the moment it is dropped, and continuing while it falls through the air, passes through the water, and ends up at rest on the bottom of the pond. Do your work on a photocopy or a printout of page 125.
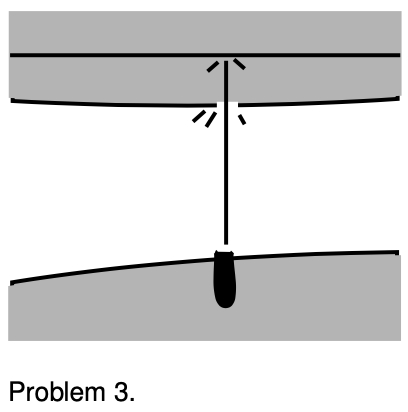 3. In an 18th-century naval battle, a cannon ball is shot horizontally, passes through the side of an enemy ship’s hull, flies across the galley, and lodges in a bulkhead. Draw plots of its horizontal position, velocity, and acceleration as functions of time, starting while it is inside the cannon and has not yet been fired, and ending when it comes to rest. There is not any significant amount of friction from the air. Although the ball may rise and fall, you are only concerned with its horizontal motion, as seen from above. Do your work on a photocopy or a printout of page 125.
3. In an 18th-century naval battle, a cannon ball is shot horizontally, passes through the side of an enemy ship’s hull, flies across the galley, and lodges in a bulkhead. Draw plots of its horizontal position, velocity, and acceleration as functions of time, starting while it is inside the cannon and has not yet been fired, and ending when it comes to rest. There is not any significant amount of friction from the air. Although the ball may rise and fall, you are only concerned with its horizontal motion, as seen from above. Do your work on a photocopy or a printout of page 125.
4. Draw graphs of position, velocity, and acceleration as functions of time for a person bunjee jumping. (In bunjee jumping, a person has a stretchy elastic cord tied to his/her ankles, and jumps off of a high platform. At the bottom of the fall, the cord brings the person up short. Presumably the person bounces up a little.) Do your work on a photocopy or a printout of page 125.
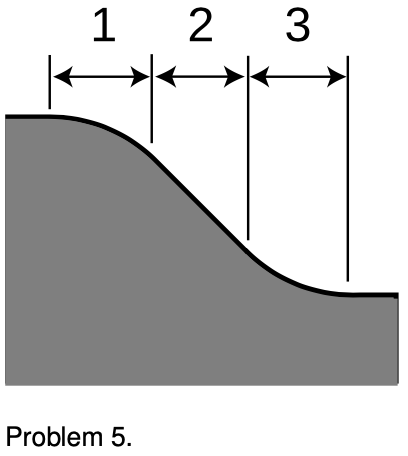 5. A ball rolls down the ramp shown in the figure, consisting of a curved knee, a straight slope, and a curved bottom. For each part of the ramp, tell whether the ball’s velocity is increasing, decreasing,
5. A ball rolls down the ramp shown in the figure, consisting of a curved knee, a straight slope, and a curved bottom. For each part of the ramp, tell whether the ball’s velocity is increasing, decreasing,
or constant, and also whether the ball’s acceleration is increasing, decreasing, or constant. Explain your answers. Assume there is no air friction or rolling resistance. Hint: Try problem 20 first. [Based
on a problem by Hewitt.]
6. A toy car is released on one side of a piece of track that is bent into an upright U shape. The car goes back and forth. When the car reaches the limit of its motion on one side, its velocity is zero. Is its acceleration also zero? Explain using a v - t graph. [Based on a problem by Serway and Faughn.]
7. What is the acceleration of a car that moves at a steady velocity of 100 km/h for 100 seconds? Explain your answer. [Based on a problem by Hewitt.]
8. A physics homework question asks, “If you start from rest and accelerate at 1.54 m/s2 for 3.29 s, how far do you travel by the end of that time?” A student answers as follows:
1.54*3.29=5.07 m
His Aunt Wanda is good with numbers, but has never taken physics. She doesn’t know the formula for the distance traveled under constant acceleration over a given amount of time, but she tells her
nephew his answer cannot be right. How does she know?
9. You are looking into a deep well. It is dark, and you cannot see the bottom. You want to find out how deep it is, so you drop a rock in, and you hear a splash 3.0 seconds later. How deep is the well?
10. You take a trip in your spaceship to another star. Setting off, you increase your speed at a constant acceleration. Once you get half-way there, you start decelerating, at the same rate, so that by the time you get there, you have slowed down to zero speed. You see the tourist attractions, and then head home by the same method. (a) Find a formula for the time, T , required for the round trip, in terms of d, the distance from our sun to the star, and a, the magnitude of the acceleration. Note that the acceleration is not constant over the whole trip, but the trip can be broken up into constant-acceleration parts.
(b) The nearest star to the Earth (other than our own sun) is Proxima Centauri, at a distance of d = 4 × 1016 m. Suppose you use an acceleration of a = 10 m/s2 , just enough to compensate for the lack of true gravity and make you feel comfortable. How long does the round trip take, in years?
(c) Using the same numbers for d and a, find your maximum speed. Compare this to the speed of light, which is 3.0 × 108 m/s. (Later in this course, you will learn that there are some new things going on in physics when one gets close to the speed of light, and that it is impossible to exceed the speed of light. For now, though, just use the simpler ideas you’ve learned so far.)
11. You climb half-way up a tree, and drop a rock. Then you climb to the top, and drop another rock. How many times greater is the velocity of the second rock on impact? Explain. (The answer is not two times greater.)
12. Alice drops a rock off a cliff. Bubba shoots a gun straight down from the edge of the same cliff. Compare the accelerations of the rock and the bullet while they are in the air on the way down. [Based on a problem by Serway and Faughn.
13. A person is parachute jumping. During the time between when she leaps out of the plane and when she opens her chute, her altitude is given by an equation of the form
`y=b-c(t+ke^(-t/k))`,
where `e` is the base of natural logarithms, and `b`,` c`, and `k` are constants. Because of air resistance, her velocity does not increase at a steady rate as it would for an object falling in vacuum.
a) What units would `b`, `c`, and `k` have to have for the equation to make sense?
(b) Find the person’s velocity, `v`, as a function of time. [You will need to use the chain rule, and the fact that `d(e x )"/" dx = e^x` .]
(c) Use your answer from part (b) to get an interpretation of the constant c. [Hint: `e^(-x)` approaches zero for large values of `x`.]
(d) Find the person’s acceleration, `a`, as a function of time.
(e) Use your answer from part (d) to show that if she waits long enough to open her chute, her acceleration will become very small.
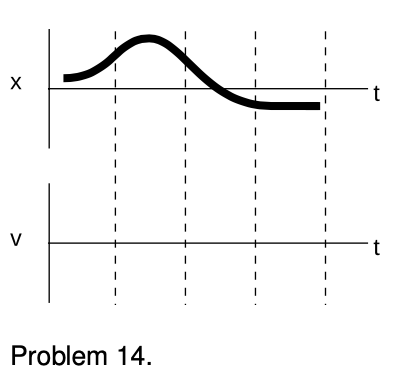 14. The top part of the figure shows the position-versus-time graph for an object moving in one dimension. On the bottom part of the figure, sketch the corresponding v-versus-t graph. `=>`Solution, p. 536
14. The top part of the figure shows the position-versus-time graph for an object moving in one dimension. On the bottom part of the figure, sketch the corresponding v-versus-t graph. `=>`Solution, p. 536
15. On New Year’s Eve, a stupid person fires a pistol straight up. The bullet leaves the gun at a speed of 100 m/s. How long does it take before the bullet hits the ground? `=>`Solution, p. 536
16. If the acceleration of gravity on Mars is 1/3 that on Earth, how many times longer does it take for a rock to drop the same distance on Mars? Ignore air resistance. `=>` Solution, p. 536
17. A honeybee’s position as a function of time is given by `x = 10t -t^3` , where t is in seconds and x in meters. What is its acceleration at t = 3.0 s? `=>` Solution, p. 536
18. In July 1999, Popular Mechanics carried out tests to find which car sold by a major auto maker could cover a quarter mile (402 meters) in the shortest time, starting from rest. Because the distance is so short, this type of test is designed mainly to favor the car with the greatest acceleration, not the greatest maximum speed (which is irrelevant to the average person). The winner was the Dodge Viper, with a time of 12.08 s. The car’s top (and presumably final) speed was 118.51 miles per hour (52.98 m/s). (a) If a car, starting from rest and moving with constant acceleration, covers a quarter mile in his time interval, what is its acceleration?
(b) What would be the final speed of a car that covered a quarter mile with the constant acceleration you found in part a?
(c) Based on the discrepancy between your answer in part b and the actual final speed of the Viper, what do you conclude about how its acceleration changed over time? `=>` Solution, p. 536
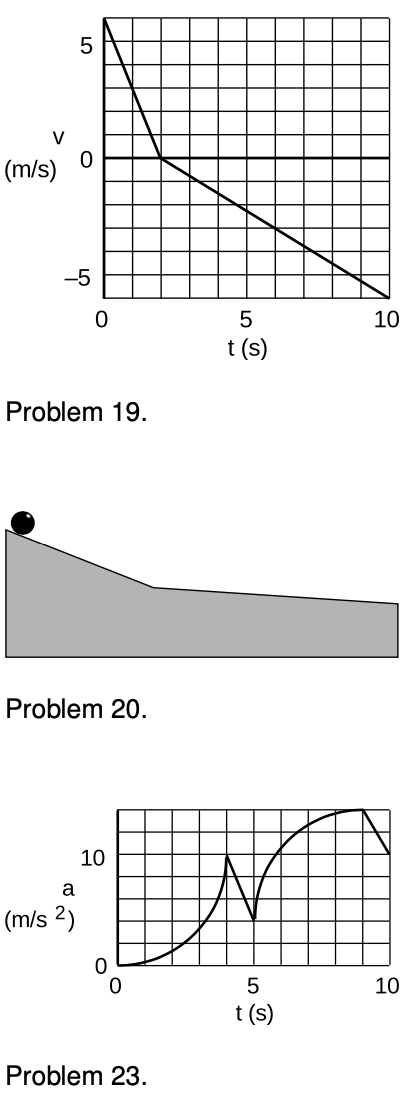 19. The graph represents the motion of a ball that rolls up a hill and then back down. When does the ball return to the location it had at t = 0? `=>` Solution, p. 536
19. The graph represents the motion of a ball that rolls up a hill and then back down. When does the ball return to the location it had at t = 0? `=>` Solution, p. 536
20. (a) The ball is released at the top of the ramp shown in the figure. Friction is negligible. Use physical reasoning to draw v - t and a - t graphs. Assume that the ball doesn’t bounce at the point where the ramp changes slope. (b) Do the same for the case where the ball is rolled up the slope from the right side, but doesn’t quite have enough speed to make it over the top. `=>` Solution, p. 536
21. You throw a rubber ball up, and it falls and bounces several times. Draw graphs of position, velocity, and acceleration as functions of time. ``=>` Solution, p. 536
22. Starting from rest, a ball rolls down a ramp, traveling a distance L and picking up a final speed v. How much of the distance did the ball have to cover before achieving a speed of v/2? [Based on a problem by Arnold Arons.]
23. The graph shows the acceleration of a chipmunk in a TV cartoon. It consists of two circular arcs and two line segments. At t = 0.00 s, the chipmunk’s velocity is -3.10 m/s. What is its velocity at t = 10.00 s?
24. Find the error in the following calculation. A student wants to find the distance traveled by a car that accelerates from rest for 5.0 s with an acceleration of `2.0 m/s2` . First he solves `a=Deltav"/"Deltat` for `Deltav` = 10 m/s. Then he multiplies to find (10 m/s)(5.0 s) = 50 m. Do not just recalculate the result by a different method; if that was all you did, you’d have no way of knowing which calculation was correct, yours or his.
25. Acceleration could be defined either as `Deltav"/"Deltat` or as the slope of the tangent line on the v - t graph. Is either one superior as a definition, or are they equivalent? If you say one is better, give an example of a situation where it makes a difference which one you use.
26. If an object starts accelerating from rest, we have `v^2=2a*Deltax` for its speed after it has traveled a distance `Deltax`. Explain in words why it makes sense that the equation has velocity squared, but distance only to the first power. Don’t recapitulate the derivation in the book, or give a justification based on units. The point is to explain what this feature of the equation tells us about the way speed increases as more distance is covered.
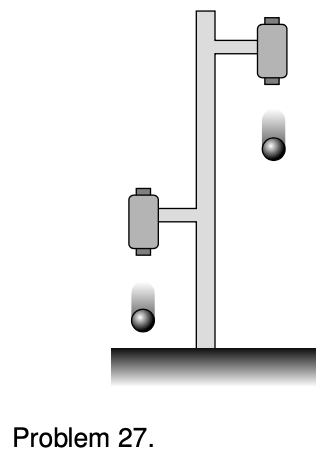 27. The figure shows a practical, simple experiment for determining g to high precision. Two steel balls are suspended from electromagnets, and are released simultaneously when the electric current is shut off. They fall through unequal heights `Deltax_1` and `Deltax_2` . A computer records the sounds through a microphone as first one ball and then the other strikes the floor. From this recording, we can accurately determine the quantity T defined as `T = Δt2 - Δt1` i.e., the time lag between the first and second impacts. Note that since the balls do not make any sound when they are released, we have no way of measuring the individual times `Deltax_1` and `Deltax_2`.
27. The figure shows a practical, simple experiment for determining g to high precision. Two steel balls are suspended from electromagnets, and are released simultaneously when the electric current is shut off. They fall through unequal heights `Deltax_1` and `Deltax_2` . A computer records the sounds through a microphone as first one ball and then the other strikes the floor. From this recording, we can accurately determine the quantity T defined as `T = Δt2 - Δt1` i.e., the time lag between the first and second impacts. Note that since the balls do not make any sound when they are released, we have no way of measuring the individual times `Deltax_1` and `Deltax_2`.
(a) Find an equation for g in terms of the measured quantities T, `Deltax_1` and `Deltax_2`.
(b) Check the units of your equation.
(c) Check that your equation gives the correct result in the case where `Deltax_1` is very close to zero. However, is this case realistic?
(d) What happens when `Deltax_1` = `Deltax_2`? Discuss this both mathematically and physically.
28. The speed required for a low-earth orbit is `7.9 × 103 m/s` (see ch. 10). When a rocket is launched into orbit, it goes up a little at first to get above almost all of the atmosphere, but then tips over horizontally to build up to orbital speed. Suppose the horizontal acceleration is limited to 3g to keep from damaging the cargo (or hurting the crew, for a crewed flight). (a) What is the minimum distance the rocket must travel downrange before it reaches orbital speed? How much does it matter whether you take into account the initial eastward velocity due to the rotation of the earth? (b) Rather than a rocket ship, it might be advantageous to use a railgun design, in which the craft would be accelerated to orbital speeds along a railroad track. This has the advantage that it isn’t necessary to lift a large mass of fuel, since the energy source is external. Based on your answer to part a, comment on the feasibility of this design for crewed launches from the earth’s surface.

29. Some fleas can jump as high as 30 cm. The flea only has a short time to build up speed — the time during which its center of mass is accelerating upward but its feet are still in contact with the ground. Make an order-of-magnitude estimate of the acceleration the flea needs to have while straightening its legs, and state your answer in units of g, i.e., how many “g’s it pulls.” (For comparison, fighter pilots black out or die if they exceed about 5 or 10 g’s.)
30. Consider the following passage from Alice in Wonderland, in which Alice has been falling for a long time down a rabbit hole:
Down, down, down. Would the fall never come to an end? “I wonder how many miles I’ve fallen by this time?” she said aloud. “I must be getting somewhere near the center of the earth. Let me see: that would be four thousand miles down, I think” (for, you see, Alice had learned several things of this sort in her lessons in the schoolroom, and though this was not a very good opportunity for showing off her knowledge, as there was no one to listen to her, still it was good practice to say it over)...
 Alice doesn’t know much physics, but let’s try to calculate the amount of time it would take to fall four thousand miles, starting from rest with an acceleration of 10 m/s 2 . This is really only a lower limit; if there really was a hole that deep, the fall would actually take a longer time than the one you calculate, both because there is air friction and because gravity gets weaker as you get deeper (at the center of the earth, g is zero, because the earth is pulling you equally in every direction at once).
Alice doesn’t know much physics, but let’s try to calculate the amount of time it would take to fall four thousand miles, starting from rest with an acceleration of 10 m/s 2 . This is really only a lower limit; if there really was a hole that deep, the fall would actually take a longer time than the one you calculate, both because there is air friction and because gravity gets weaker as you get deeper (at the center of the earth, g is zero, because the earth is pulling you equally in every direction at once).
31. The photo shows Apollo 16 astronaut John Young jumping on the moon and saluting at the top of his jump. The video footage of the jump shows him staying aloft for 1.45 seconds. Gravity on the moon is 1/6 as strong as on the earth. Compute the height of the jump.
 32. Most people don’t know that Spinosaurus aegyptiacus, not Tyrannosaurus rex, was the biggest theropod dinosaur. We can’t put a dinosaur on a track and time it in the 100 meter dash, so we can only infer from physical models how fast it could have run. When an animal walks at a normal pace, typically its legs swing more or less like pendulums of the same length . As a further simplification of this model, let’s imagine that the leg simply moves at a fixed acceleration as it falls to the ground. That is, we model the time for a quarter of a stride cycle as being the same as the time required for free fall from a height . S. aegyptiacus had legs about four times longer than those of a human. (a) Compare the time required for a human’s stride cycle to that for S. aegyptiacus. (b) Compare their running speeds.
32. Most people don’t know that Spinosaurus aegyptiacus, not Tyrannosaurus rex, was the biggest theropod dinosaur. We can’t put a dinosaur on a track and time it in the 100 meter dash, so we can only infer from physical models how fast it could have run. When an animal walks at a normal pace, typically its legs swing more or less like pendulums of the same length . As a further simplification of this model, let’s imagine that the leg simply moves at a fixed acceleration as it falls to the ground. That is, we model the time for a quarter of a stride cycle as being the same as the time required for free fall from a height . S. aegyptiacus had legs about four times longer than those of a human. (a) Compare the time required for a human’s stride cycle to that for S. aegyptiacus. (b) Compare their running speeds.
33. Engineering professor Qingming Li used sensors and video cameras to study punches delivered in the lab by British former welterweight boxing champion Ricky “the Hitman” Hatton. For comparison, Li also let a TV sports reporter put on the gloves and throw punches. The time it took for Hatton’s best punch to arrive, i.e., the time his opponent would have had to react, was about 0.47
of that for the reporter. Let’s assume that the fist starts from rest and moves with constant acceleration all the way up until impact, at some fixed distance (arm’s length). Compare Hatton’s acceleration to the reporter’s.
34. Aircraft carriers originated in World War I, and the first landing on a carrier was performed by E.H. Dunning in a Sopwith Pup biplane, landing on HMS Furious. (Dunning was killed the second time he attempted the feat.) In such a landing, the pilot slows down to just above the plane’s stall speed, which is the minimum speed at which the plane can fly without stalling. The plane then lands and is caught by cables and decelerated as it travels the length of the flight deck. Comparing a modern US F-14 fighter jet landing on an Enterprise-class carrier to Dunning’s original exploit, the stall speed is greater by a factor of 4.8, and to accommodate this, the length of the flight deck is greater by a factor of 1.9. Which deceleration is greater, and by what factor?
35. In college-level women’s softball in the U.S., typically a pitcher is expected to be at least 1.75 m tall, but Virginia Tech pitcher Jasmin Harrell is 1.62 m. Although a pitcher actually throws by stepping forward and swinging her arm in a circle, let’s make a simplified physical model to estimate how much of a disadvantage Harrell has had to overcome due to her height. We’ll pretend that the pitcher gives the ball a constant acceleration in a straight line, and that the length of this line is proportional to the pitcher’s height. Compare the acceleration Harrell would have to supply with the acceleration that would suffice for a pitcher of the nominal minimum height, if both were to throw a pitch at the same speed.
 36. When the police engage in a high-speed chase on city streets, it can be extremely dangerous both to the police and to other motorists and pedestrians. Suppose that the police car must travel at a speed that is limited by the need to be able to stop before hitting a baby carriage, and that the distance at which the driver first sees the baby carriage is fixed. Tests show that in a panic stop from high speed, a police car based on a Chevy Impala has a deceleration 9% greater than that of a Dodge Intrepid. Compare the maximum safe speeds for the two cars.
36. When the police engage in a high-speed chase on city streets, it can be extremely dangerous both to the police and to other motorists and pedestrians. Suppose that the police car must travel at a speed that is limited by the need to be able to stop before hitting a baby carriage, and that the distance at which the driver first sees the baby carriage is fixed. Tests show that in a panic stop from high speed, a police car based on a Chevy Impala has a deceleration 9% greater than that of a Dodge Intrepid. Compare the maximum safe speeds for the two cars.
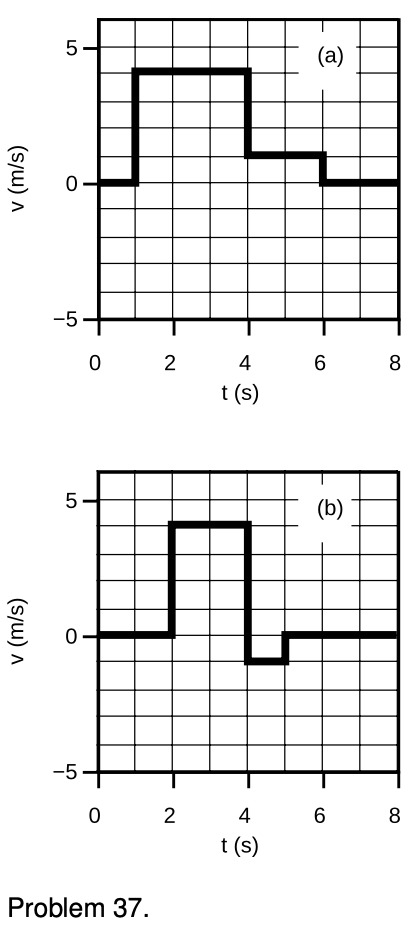
37. For each of the two graphs, find the change in position `Deltax` from beginning to end, using the technique described in section 3.5.
The following form can be used for the homework problems that require sketching a set of graphs.

3.9 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.