3.4 Varying acceleration by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
3.4 Varying acceleration
So far we have only been discussing examples of motion for which the v-t graph is linear. If we wish to generalize our definition to v-t graphs that are more complex curves, the best way to proceed is similar to how we defined velocity for curved x-t graphs:
definition of acceleration
The acceleration of an object at any instant is the slope of the tangent line passing through its `v`-versus-`t` graph at the relevant point.
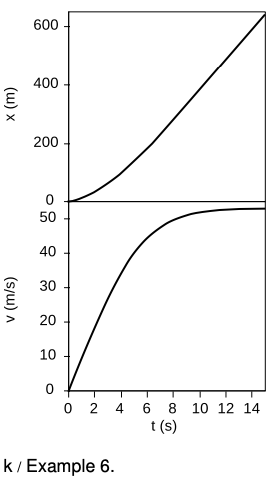 Example 6: A skydiver
Example 6: A skydiver
⇒ The graphs in figure k show the results of a fairly realistic computer simulation of the motion of a skydiver, including the effects of air friction. The x axis has been chosen pointing down, so x is increasing as she falls. Find (a) the skydiver's acceleration at t=3.0 s, and also (b) at t=7.0 s.
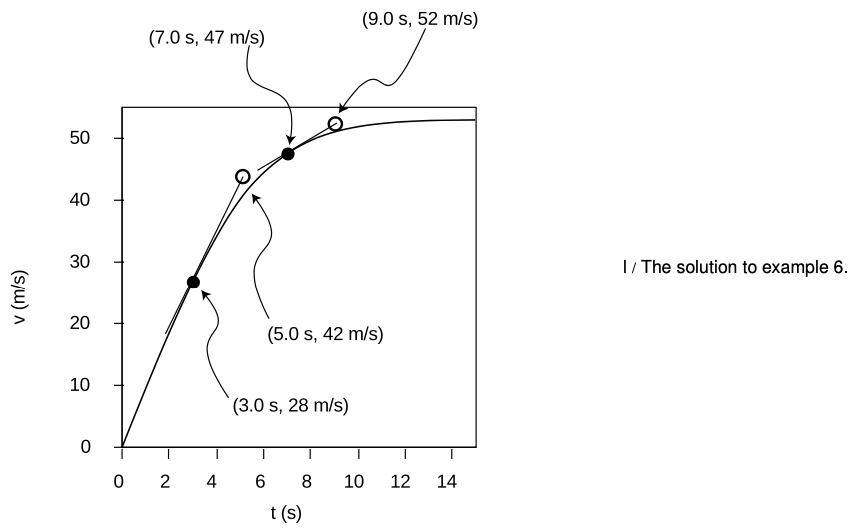
⇒ The solution is shown in figure l. I've added tangent lines at the two points in question.
(a) To find the slope of the tangent line, I pick two points on the line (not necessarily on the actual curve): (3.0 s, 28m/s) and (5.0 s,42 m/s)`. The slope of the tangent line is (42 m/s - 28 m/s) / (5.0 s - 3.0 s) = 7.0 m/ s2.
(b) Two points on this tangent line are (7.0 s, 47 m/s) and (9.0 s,52 m/s). The slope of the tangent line is (52 m/s - 47 m/s) / (9.0 s - 7.0 s) = 2.5 m/s2.
Physically, what's happening is that at t=3.0 s, the skydiver is not yet going very fast, so air friction is not yet very strong. She therefore has an acceleration almost as great as g. At t=7.0 s, she is moving almost twice as fast (about 100 miles per hour), and air friction is extremely strong, resulting in a significant departure from the idealized case of no air friction.
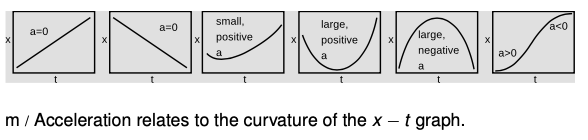
In example 6, the x-t graph was not even used in the solution of the problem, since the definition of acceleration refers to the slope of the v-t graph. It is possible, however, to interpret an x-t graph to find out something about the acceleration. An object with zero acceleration, i.e., constant velocity, has an x-t graph that is a straight line. A straight line has no curvature. A change in velocity requires a change in the slope of the x-t graph, which means that it is a curve rather than a line. Thus acceleration relates to the curvature of the x-t graph. Figure m shows some examples.
In example 6, the x-t graph was more strongly curved at the beginning, and became nearly straight at the end. If the x-t graph is nearly straight, then its slope, the velocity, is nearly constant, and the acceleration is therefore small. We can thus interpret the acceleration as representing the curvature of the x-t graph, as shown in figure m. If the “cup” of the curve points up, the acceleration is positive, and if it points down, the acceleration is negative.
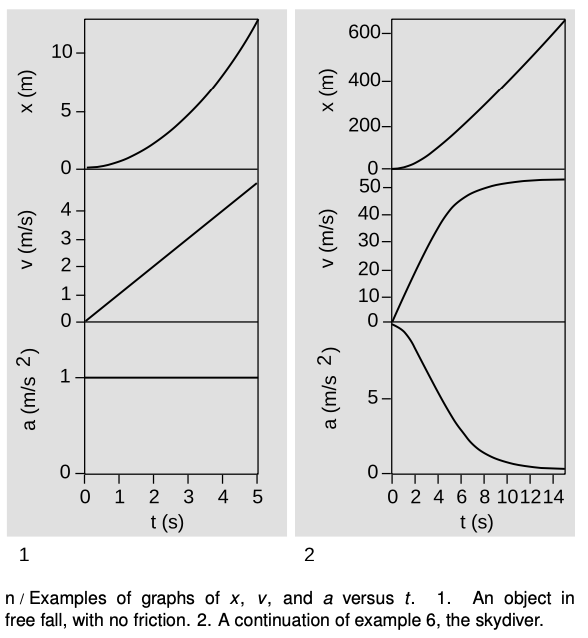
Since the relationship between `a` and `v` is analogous to the relationship between `v` and `x`, we can also make graphs of acceleration as a function of time, as shown in figure n.
 ⇒ Solved problem: Drawing a v-t graph. — problem 14
⇒ Solved problem: Drawing a v-t graph. — problem 14
⇒ Solved problem: Drawing v-t and a-t graphs. — problem 20
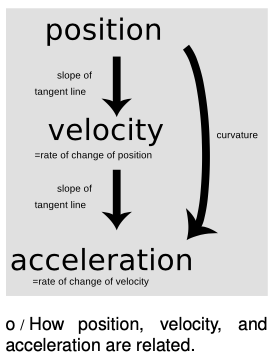
Figure o summarizes the relationships among the three types of graphs.
Discussion Questions
A Describe in words how the changes in the a-t graph in figure n and relate to the behavior of the v-t graph.
B Explain how each set of graphs contains inconsistencies, and fix them.
C In each case, pick a coordinate system and draw x-t, v-t, and a-t graphs. Picking a coordinate system means picking where you want x=0 to be, and also picking a direction for the positive x axis.
(1) An ocean liner is cruising in a straight line at constant speed.
(2) You drop a ball. Draw two different sets of graphs (a total of 6), with one set's positive `x` axis pointing in the opposite direction compared to the other's.
(3) You're driving down the street looking for a house you've never been to before. You realize you've passed the address, so you slow down, put the car in reverse, back up, and stop in front of the house.
3.4 Varying acceleration by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.