2.5 Addition of velocities by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
2.5 Addition of velocities
Addition of velocities to describe relative motion
Since absolute motion cannot be unambiguously measured, the only way to describe motion unambiguously is to describe the motion of one object relative to another. Symbolically, we can write `v_(PQ)` for the velocity of object `P` relative to object `Q`.
Velocities measured with respect to different reference points can be compared by addition. In the figure below, the ball's velocity relative to the couch equals the ball's velocity relative to the truck plus the truck's velocity relative to the couch:
` =5 cm"/"s+10 cm"/"s`
`=15 cm"/"s`
The same equation can be used for any combination of three objects, just by substituting the relevant subscripts for B, T, and C. Just remember to write the equation so that the velocities being added have the same subscript twice in a row. In this example, if you read off the subscripts going from left to right, you get BC...=...BTTC. The fact that the two “inside” subscripts on the right are the same means that the equation has been set up correctly. Notice how subscripts on the left look just like the subscripts on the right, but with the two T's eliminated.
Negative velocities in relative motion
My discussion of how to interpret positive and negative signs of velocity may have left you wondering why we should bother. Why not just make velocity positive by definition? The original reason why negative numbers were invented was that bookkeepers decided it would be convenient to use the negative number concept for payments to distinguish them from receipts. It was just plain easier than writing receipts in black and payments in red ink. After adding up your month's positive receipts and negative payments, you either got a positive number, indicating profit, or a negative number, showing a loss. You could then show that total with a high-tech “`+`” or “`-`” sign, instead of looking around for the appropriate bottle of ink.
Nowadays we use positive and negative numbers for all kinds of things, but in every case the point is that it makes sense to add and subtract those things according to the rules you learned in grade school, such as “minus a minus makes a plus, why this is true we need not discuss.” Adding velocities has the significance of comparing relative motion, and with this interpretation negative and positive velocities can be used within a consistent framework.

For example, the truck's velocity relative to the couch equals the truck's velocity relative to the ball plus the ball's velocity relative to the couch:
`v_(TC)`=`v_(BT)`+`v_(BC)`
`=- 5 cm"/"s+15 cm"/"s`
`=10 cm"/"s`
If we didn't have the technology of negative numbers, we would have had to remember a complicated set of rules for adding velocities: (1) if the two objects are both moving forward, you add, (2) if one is moving forward and one is moving backward, you subtract, but (3) if they're both moving backward, you add. What a pain that would have been.
`=>` Solved problem: two dimensions — problem 10
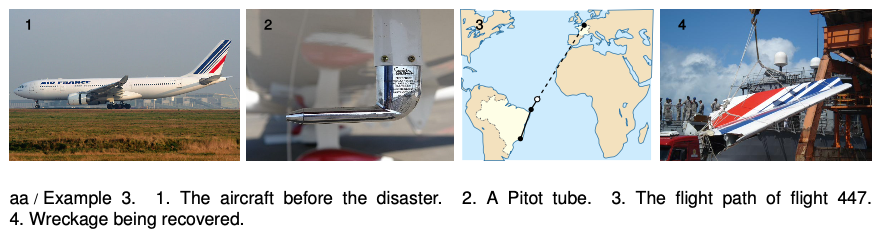
Example 3: Airspeed
On June 1, 2009, Air France flight 447 disappeared without warning over the Atlantic Ocean. All 232 people aboard were killed. Investigators believe the disaster was triggered because the pilots lost the ability to accurately determine their speed relative to the air. This is done using sensors called Pitot tubes, mounted outside the plane on the wing. Automated radio signals showed that these sensors gave conflicting readings before the crash, possibly because they iced up. For fuel efficiency, modern passenger jets fly at a very high altitude, but in the thin air they can only fly within a very narrow range of speeds. If the speed is too low, the plane stalls, and if it's too high, it breaks up. If the pilots can't tell what their airspeed is, they can't keep it in the safe range.
Many people's reaction to this story is to wonder why planes don't just use GPS to measure their speed. One reason is that GPS tells you your speed relative to the ground, not relative to the air. Letting P be the plane, A the air, and G the ground, we have
where `v_(PG)` (the “true ground speed”) is what GPS would measure, `v_(PA)` (“airspeed”) is what's critical for stable flight, and `v_(AG)` is the velocity of the wind relative to the ground 9000 meters below. Knowing `v_(PG)` isn't enough to determine `v_(PA)` unless `v_(AG)` is also known.
Discussion Questions
A Interpret the general rule `v_(AB) = - v_(BA)` in words.
B Wa-Chuen slips away from her father at the mall and walks up the down escalator, so that she stays in one place. Write this in terms of symbols.
2.5 Addition of velocities by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.