2.3 Graphs of motion; velocity by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
2.3 Graphs of motion; velocity
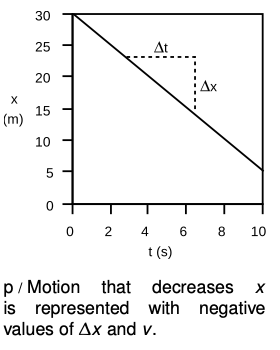 Motion with constant velocity
Motion with constant velocity
In example o, an object is moving at constant speed in one direction. We can tell this because every two seconds, its position changes by five meters.
In algebra notation, we'd say that the graph of x vs. t shows the same change in position, Δx =5.0 m, over each interval of Δt =2.0 s. The object's velocity or speed is obtained by calculating `v = (Delta x)`/`(Delta t)`=`(5.0 "m")"/"(2.0 "s")=2.5 "m/s"`. In graphical terms, the velocity can be interpreted as the slope of the line. Since the graph is a straight line, it wouldn't have mattered if we'd taken a longer time interval and calculated `v=Deltax"/"Deltat``=(10.0m)"/"(4.0s)`. The answer would still have been the same, `2.5m"/"s`.
 Note that when we divide a number that has units of meters by another number that has units of seconds, we get units of meters per second, which can be written m/s. This is another case where we treat units as if they were algebra symbols, even though they're not.
Note that when we divide a number that has units of meters by another number that has units of seconds, we get units of meters per second, which can be written m/s. This is another case where we treat units as if they were algebra symbols, even though they're not.
In example p, the object is moving in the opposite direction: as time progresses, its x coordinate decreases. Recalling the definition of the `Delta` notation as “after minus before,” we find that Δt is still positive, but Δx must be negative. The slope of the line is therefore negative, and we say that the object has a negative velocity ( `v=Deltax"/"Deltat`)= `(−5.0 m)"/"(2.0 s) = −2.5 m"/"s`. We’ve already seen that the plus and minus signs of ?x values have the interpretation of telling us which direction the object moved. Since ?t is always positive, dividing by ?t doesn’t change the plus or minus sign, and the plus and minus signs of velocities are to be interpreted in the same way. In graphical terms, 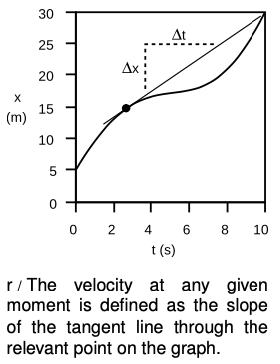 a positive slope characterizes a line that goes up as we go to the right, and a negative slope tells us that the line went down as we went to the right.
a positive slope characterizes a line that goes up as we go to the right, and a negative slope tells us that the line went down as we went to the right.
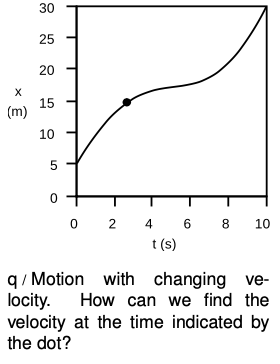
Motion with changing velocity
Now what about a graph like figure q? This might be a graph of a car’s motion as the driver cruises down the freeway, then slows down to look at a car crash by the side of the road, and then speeds up again, disappointed that there is nothing dramatic going on such as flames or babies trapped in their car seats. (Note that we are still talking about one-dimensional motion. Just because the graph is curvy doesn’t mean that the car’s path is curvy. The graph is not like a map, and the horizontal direction of the graph represents the passing of time, not distance.) Example q is similar to example o in that the object moves a total of 25.0 m in a period of 10.0 s, but it is no longer true that it makes the same amount of progress every second. There is no way to characterize the entire graph by a certain velocity or slope, because the velocity is different at every moment. It would be incorrect to say that because the car covered 25.0 m in 10.0 s, its velocity was 2.5 m/s. It moved faster than that at the beginning and end, but slower in the middle. There may have been certain instants at which the car was indeed going 2.5 m/s, but the speedometer swept past that value without “sticking,” just as it swung through various other values of speed. (I definitely want my next car to have a speedometer calibrated in m/s and showing both negative and positive values.) We assume that our speedometer tells us what is happening to the speed of our car at every instant, but how can we define speed mathematically in a case like this? We can’t just define it as the slope of the curvy graph, because a curve doesn’t have a single well-defined slope as does a line. A mathematical definition that corresponded to the speedometer reading would have to be one that assigned a velocity value to a single point on the curve, i.e., a single instant in time, rather than to the entire graph. If we wish to define the speed at one instant such as the one marked with a dot, the best way to proceed is illustrated in r, where we have drawn the line through that point called the tangent line, the line that “hugs the curve.” We can then adopt the following definition of velocity:

One interpretation of this definition is that the velocity tells us how many meters the object would have traveled in one second, if it had continued moving at the same speed for at least one second
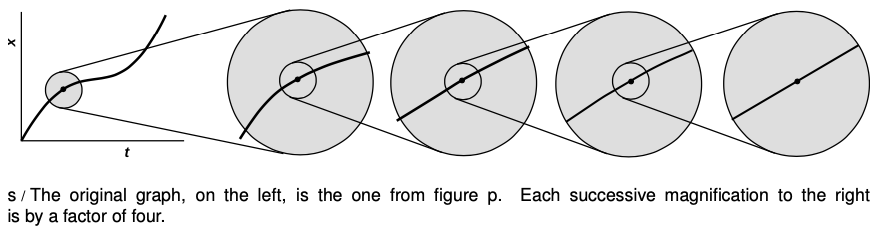
A good way of thinking about the tangent-line definition is shown in figure s. We zoom in on our point of interest more and more, as if through a microscope capable of unlimited magnification. As we zoom in, the curviness of the graph becomes less and less apparent. (Similarly, we don’t notice in everyday life that the earth is a sphere.) In the figure, we zoom in by 400%, and then again by 400%, and so on. After a series of these zooms, the graph appears indistinguishable from a line, and we can measure its slope just as we would for a line. If all we saw was the ultra-magnified view, we would assume that the object was moving at a constant speed, which is 2.5 m/s in our example, and that it would continue to move at that speed. Therefore the speed of 2.5 m/s can be interpreted as meaning that if the object had continued at constant speed for a further time interval of 1 s, it would have traveled 2.5 m.
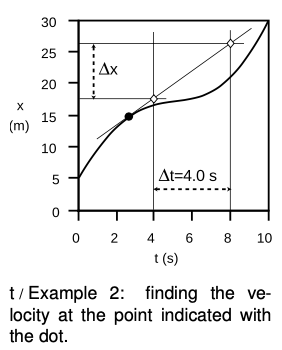 Example 2: The slope of the tangent line
Example 2: The slope of the tangent line
`=>` What is the velocity at the point shown with a dot on the graph?
`=>` First we draw the tangent line through that point. To find the slope of the tangent line, we need to pick two points on it. Theoretically, the slope should come out the same regardless of which two points we pick, but in practical terms we'll be able to measure more accurately if we pick two points fairly far apart, such as the two white diamonds. To save work, we pick points that are directly above labeled points on the t axis, so that `Deltat=4.0s` is easy to read off. One diamond lines up with `xapprox17.5m`, the other with `xapprox26.5m`, so `Deltax`=9.0 m. The velocity is `Deltax"/"Deltat=2.2 m"/"s`.
Looking at the tangent line in figure t, we can see that it touches the curve at the point marked with a dot, but without cutting through it at that point. No other line through that point has this “no-cut” property; if we rotated the line either clockwise or counterclockwise about the point, it would cut through. Except in certain unusual cases, there is always exactly one such no-cut line at any given point on a smooth curve, and that no-cut line is the tangent line. It's as though the region below the curve were a solid block of wood, and the tangent line were the edge of a ruler. The ruler can't penetrate the block.
Conventions about graphing
The placement of t on the horizontal axis and x on the upright axis may seem like an arbitrary convention, or may even have disturbed you, since your algebra teacher always told you that x goes on the horizontal axis and y goes on the upright axis. There is a reason for doing it this way, however. In example t, we have an object that reverses its direction of motion twice. It can only be in one place at any given time, but there can be more than one time when it is at a given place. For instance, this object passed through `x=17m` on three separate occasions, but there is no way it could have been in more than one place at `t=5.0s`. Resurrecting some terminology you learned in your trigonometry course, we say that x is a function of t, but t is not a function of x. In situations such as this, there is a useful convention that the graph should be oriented so that any vertical line passes through the curve at only one point. Putting the x axis across the page and t upright would have violated this convention. To people who are used to interpreting graphs, a graph that violates this convention is as annoying as fingernails scratching on a chalkboard. We say that this is a graph of “x versus t.” If the axes were the other way around, it would be a graph of “t versus x.” I remember the “versus” terminology by visualizing the labels on the x and t axes and remembering that when you read, you go from left to right and from top to bottom.
Discussion Questions
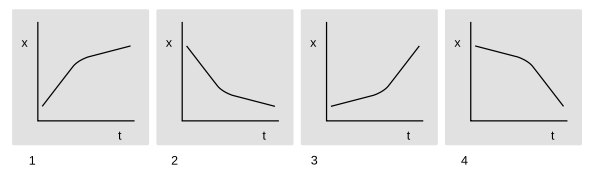
A Park is running slowly in gym class, but then he notices Jenna watching him, so he speeds up to try to impress her. Which of the graphs could represent his motion?
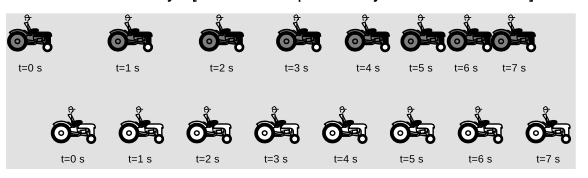
 B The figure shows a sequence of positions for two racing tractors. Compare the tractors' velocities as the race progresses. When do they have the same velocity? [Based on a question by Lillian McDermott.]
B The figure shows a sequence of positions for two racing tractors. Compare the tractors' velocities as the race progresses. When do they have the same velocity? [Based on a question by Lillian McDermott.]
C If an object had an x-t graph that was a straight line with `Deltax=0` and `Deltat!=0`, what would you say about its velocity? Sketch an example of such a graph. What about `Deltat=0` and `Deltax!=0`?
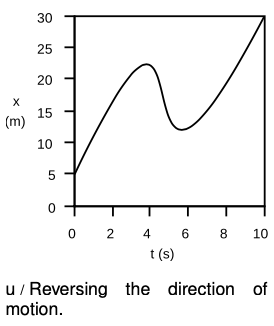
D If an object has a wavy motion graph like the one in figure u on p. 78, what are the times at which the object reverses its direction? Describe the object's velocity at these points.
E Discuss anything unusual about the following three graphs.
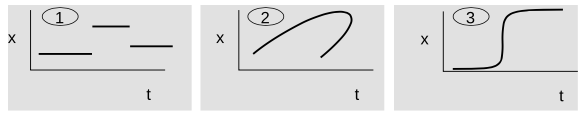
F I have been using the term “velocity” and avoiding the more common English word “speed,” because introductory physics texts typically define them to mean different things. They use the word “speed,” and the symbol “s” to mean the absolute value of the velocity, `s=|v|`. Although I've chosen not to emphasize this distinction in technical vocabulary, there are clearly two different concepts here. Can you think of an example of a graph of x-versus-t in which the object has constant speed, but not constant velocity?
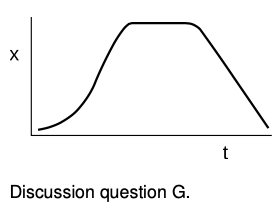 G For the graph shown in the figure, describe how the object's velocity changes.
G For the graph shown in the figure, describe how the object's velocity changes.
H Two physicists duck out of a boring scientific conference. On the street, they witness an accident in which a pedestrian is injured by a hit-and-run driver. A criminal trial results, and they must testify. In her testimony, Dr. Transverz Waive says, “The car was moving along pretty fast, I'd say the velocity was `+40mi"/"hr`. They saw the old lady too late, and even though they slammed on the brakes they still hit her before they stopped. Then they made a U turn and headed off at a velocity of about `-20mi"/"hr`, I'd say.” Dr. Longitud N.L. Vibrasheun says, “He was really going too fast, maybe his velocity was `-35` or `-40mi"/"hr`. After he hit Mrs. Hapless, he turned around and left at a velocity of, oh, I'd guess maybe `+20` or `+25mi"/"hr`.” Is their testimony contradictory? Explain.
2.3 Graphs of motion; velocity by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.{{/equation_solver_popup}}