2.2 Describing distance and time by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
2.2 Describing distance and time
Center-of-mass motion in one dimension is particularly easy to deal with because all the information about it can be encapsulated in two variables: `x`, the position of the center of mass relative to the origin, and `t`, which measures a point in time. For instance, if someone supplied you with a sufficiently detailed table of `x` and `t` values, you would know pretty much all there was to know about the motion of the object's center of mass.
A point in time as opposed to duration
`Deltat`=3 hours -1 hour=2 hours.
To avoid the use of negative numbers for `Deltat`, we write the clock reading “after” to the left of the minus sign, and the clock reading “before” to the right of the minus sign. A more specific definition of the delta notation is therefore that delta stands for “after minus before.”
Even though our definition of the delta notation guarantees that `Deltat` is positive, there is no reason why `t` can't be negative. If `t` could not be negative, what would have happened one second before `t=0`? That doesn't mean that time “goes backward” in the sense that adults can shrink into infants and retreat into the womb. It just means that we have to pick a reference point and call it `t=0`, and then times before that are represented by negative values of `t`. An example is that a year like 2007 A.D. can be thought of as a positive `t` value, while one like 370 B.C. is negative. Similarly, when you hear a countdown for a rocket launch, the phrase “t minus ten seconds” is a way of saying` t= -10 s`, where `t=0` is the time of blastoff, and `t>0` refers to times after launch.
Although a point in time can be thought of as a clock reading, it is usually a good idea to avoid doing computations with expressions such as “2:35” that are combinations of hours and minutes. Times can instead be expressed entirely in terms of a single unit, such as hours. Fractions of an hour can be represented by decimals rather than minutes, and similarly if a problem is being worked in terms of minutes, decimals can be used instead of seconds.
self-check:Of the following phrases, which refer to points in time, which refer to time intervals, and which refer to time in the abstract rather than as a measurable number?
(1) “The time has come.”
(2) “Time waits for no man.”
(3) “The whole time, he had spit on his chin.”
(answer in the back of the PDF version of the book)
Position as opposed to change in position
As with time, a distinction should be made between a point in space, symbolized as a coordinate `x`, and a change in position, symbolized as `Deltax`.
As with `t,x` can be negative. If a train is moving down the tracks, not only do you have the freedom to choose any point along the tracks and call it `x=0`, but it's also up to you to decide which side of the `x=0` point is positive `x` and which side is negative `x`.
Since we've defined the delta notation to mean “after minus before,” it is possible that `Deltax` will be negative, unlike `Deltat` which is guaranteed to be positive. Suppose we are describing the motion of a train on tracks linking Tucson and Chicago. As shown in the figure, it is entirely up to you to decide which way is positive.
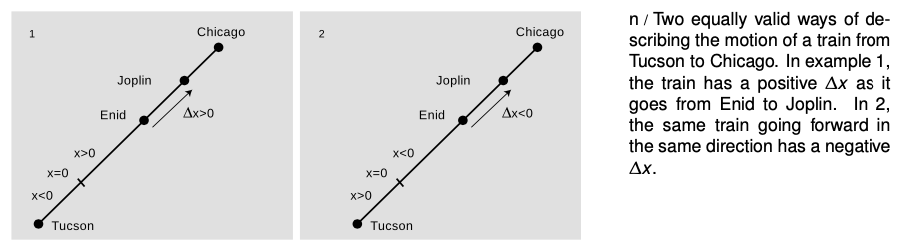
Note that in addition to `x` `Deltax`, there is a third quantity we could define, which would be like an odometer reading, or actual distance traveled. If you drive 10 miles, make a U-turn, and drive back 10 miles, then your `Deltax` is zero, but your car's odometer reading has increased by 20 miles. However important the odometer reading is to car owners and used car dealers, it is not very important in physics, and there is not even a standard name or notation for it. The change in position, `Deltax`, is more useful because it is so much easier to calculate: to compute `Deltax`, we only need to know the beginning and ending positions of the object, not all the information about how it got from one position to the other.
self-check:A ball falls vertically, hits the floor, bounces to a height of one meter, falls, and hits the floor again. Is the `Deltax` between the two impacts equal to zero, one, or two meters?
(answer in the back of the PDF version of the book)
Frames of reference
 The example above shows that there are two arbitrary choices you have to make in order to define a position variable, `x`. You have to decide where to put `x=0`, and also which direction will be positive. This is referred to as choosing a coordinate system or choosing a frame of reference. (The two terms are nearly synonymous, but the first focuses more on the actual `x` variable, while the second is more of a general way of referring to one's point of view.) As long as you are consistent, any frame is equally valid. You just don't want to change coordinate systems in the middle of a calculation.
The example above shows that there are two arbitrary choices you have to make in order to define a position variable, `x`. You have to decide where to put `x=0`, and also which direction will be positive. This is referred to as choosing a coordinate system or choosing a frame of reference. (The two terms are nearly synonymous, but the first focuses more on the actual `x` variable, while the second is more of a general way of referring to one's point of view.) As long as you are consistent, any frame is equally valid. You just don't want to change coordinate systems in the middle of a calculation.
Have you ever been sitting in a train in a station when suddenly you notice that the station is moving backward? Most people would describe the situation by saying that you just failed to notice that the train was moving --- it only seemed like the station was moving. But this shows that there is yet a third arbitrary choice that goes into choosing a coordinate system: valid frames of reference can differ from each other by moving relative to one another. It might seem strange that anyone would bother with a coordinate system that was moving relative to the earth, but for instance the frame of reference moving along with a train might be far more convenient for describing things happening inside the train.
2.2 Describing distance and time by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.