1.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary Notation
`prop` — is proportional to
~ — on the order of, is on the order of
Summary
Nature behaves differently on large and small scales. Galileo showed that this results fundamentally from the way area and volume scale. Area scales as the second power of length, `ApropL^2`, while volume scales as length to the third power, `VpropL^3`.
An order of magnitude estimate is one in which we do not attempt or expect an exact answer. The main reason why the uninitiated have trouble with order-of-magnitude estimates is that the human brain does not intuitively make accurate estimates of area and volume. Estimates of area and volume should be approached by first estimating linear dimensions, which one's brain has a feel for.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. How many cubic inches are there in a cubic foot? The answer is not 12 `sqrt`
2. Assume a dog's brain is twice as great in diameter as a cat's, but each animal's brain cells are the same size and their brains are the same shape. In addition to being a far better companion and much nicer to come home to, how many times more brain cells does a dog have than a cat? The answer is not 2.
3. The population density of Los Angeles is about `4000 "people""/"km^2`. That of San Francisco is about `6000 "people/km"^2`. How many times farther away is the average person's nearest neighbor in LA than in San Francisco? The answer is not 1.5. `sqrt`
4. A hunting dog's nose has about 10 square inches of active surface. How is this possible, since the dog's nose is only about `1 "in" × 1 "in" × 1 "in" = 1 "in"^3`? After all, 10 is greater than 1, so how can it fit?
5. Estimate the number of blades of grass on a football field.
6. In a computer memory chip, each bit of information (a 0 or a 1) is stored in a single tiny circuit etched onto the surface of a silicon chip. The circuits cover the surface of the chip like lots in a housing development. A typical chip stores 64 Mb (megabytes) of data, where a byte is 8 bits. Estimate (a) the area of each circuit, and (b) its linear size.
7. Suppose someone built a gigantic apartment building, measuring `10 "km" × 10 "km"` at the base. Estimate how tall the building would have to be to have space in it for the entire world's population to live.
8. A hamburger chain advertises that it has sold 10 billion Bongo Burgers. Estimate the total mass of feed required to raise the cows used to make the burgers.
9. Estimate the volume of a human body, in `cm^3`.
10 (solution in the pdf version of the book) How many `"cm"^2` is 1 `"mm"^2`?
11 Compare the light-gathering powers of a 3-cm-diameter telescope and a 30-"cm" telescope.
12. (solution in the pdf version of the book) One step on the Richter scale corresponds to a factor of 100 in terms of the energy absorbed by something on the surface of the Earth, e.g., a house. For instance, a 9.3-magnitude quake would release 100 times more energy than an 8.3. The energy spreads out from the epicenter as a wave, and for the sake of this problem we'll assume we're dealing with seismic waves that spread out in three dimensions, so that we can visualize them as hemispheres spreading out under the surface of the earth. If a certain 7.6-magnitude earthquake and a certain 5.6-magnitude earthquake produce the same amount of vibration where I live, compare the distances from my house to the two epicenters.
13. In Europe, a piece of paper of the standard size, called A4, is a little narrower and taller than its American counterpart. The ratio of the height to the width is the square root of 2, and this has some useful properties. For instance, if you cut an A4 sheet from left to right, you get two smaller sheets that have the same proportions. You can even buy sheets of this smaller size, and they're called A5. There is a whole series of sizes related in this way, all with the same proportions. (a) Compare an A5 sheet to an A4 in terms of area and linear size. (b) The series of paper sizes starts from an A0 sheet, which has an area of one square meter. Suppose we had a series of boxes defined in a similar way: the B0 box has a volume of one cubic meter, two B1 boxes fit exactly inside an B0 box, and so on. What would be the dimensions of a B0 box? `sqrt`
 14. Estimate the mass of one of the hairs in Albert Einstein's moustache, in units of kg.
14. Estimate the mass of one of the hairs in Albert Einstein's moustache, in units of kg.
15. According to folklore, every time you take a breath, you are inhaling some of the atoms exhaled in Caesar's last words. Is this true? If so, how many?
16. The Earth's surface is about 70% water. Mars's diameter is about half the Earth's, but it has no surface water. Compare the land areas of the two planets. `sqrt`
17. The traditional Martini glass is shaped like a cone with the point at the bottom. Suppose you make a Martini by pouring vermouth into the glass to a depth of 3 cm, and then adding gin to bring the depth to 6 cm. What are the proportions of gin and vermouth?
18. The central portion of a CD is taken up by the hole and some surrounding clear plastic, and this area is unavailable for storing data. The radius of the central circle is about 35% of the outer radius of the data-storing area. What percentage of the CD's area is therefore lost? (answer check available at lightandmatter.com)
 19. The one-liter cube in the photo has been marked off into smaller cubes, with linear dimensions one tenth those of the big one. What is the volume of each of the small cubes?
19. The one-liter cube in the photo has been marked off into smaller cubes, with linear dimensions one tenth those of the big one. What is the volume of each of the small cubes?
20. [This problem is now problem 0-12 on p. 38.]
21. Estimate the number of man-hours required for building the Great Wall of China.
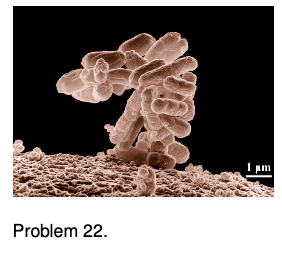 22. (a) Using the microscope photo in the figure, estimate the mass of a one cell of the E. coli bacterium, which is one of the most common ones in the human intestine. Note the scale at the lower right corner, which is `1 mum`. Each of the tubular objects in the column is one cell. (b) The feces in the human intestine are mostly bacteria (some dead, some alive), of which E. coliis a large and typical component. Estimate the number of bacteria in your intestines, and compare with the number of human cells in your body, which is believed to be roughly on the order of `10^13`. (c) Interpreting your result from part b, what does this tell you about the size of a typical human cell compared to the size of a typical bacterial cell?
22. (a) Using the microscope photo in the figure, estimate the mass of a one cell of the E. coli bacterium, which is one of the most common ones in the human intestine. Note the scale at the lower right corner, which is `1 mum`. Each of the tubular objects in the column is one cell. (b) The feces in the human intestine are mostly bacteria (some dead, some alive), of which E. coliis a large and typical component. Estimate the number of bacteria in your intestines, and compare with the number of human cells in your body, which is believed to be roughly on the order of `10^13`. (c) Interpreting your result from part b, what does this tell you about the size of a typical human cell compared to the size of a typical bacterial cell?
23. A taxon (plural taxa) is a group of living things. For example,Homo sapiens and Homo neanderthalensis are both taxa --- specifically, they are two different species within the genus Homo. Surveys by botanists show that the number of plant taxa native to a given contiguous land area `A` is usually approximately proportional to `A^(1"/"3)`. (a) There are 70 different species of lupine native to Southern California, which has an area of about `200,000 km^2`. The San Gabriel Mountains cover about `1,600 km^2`. Suppose that you wanted to learn to identify all the species of lupine in the San Gabriels. Approximately how many species would you have to familiarize yourself with?\hwans{hwans:taxa-scaling}(answer check available at lightandmatter.com)
(b) What is the interpretation of the fact that the exponent, `1"/"3`, is less than one?
24. X-ray images aren't only used with human subjects but also, for example, on insects and flowers. In 2003, a team of researchers at Argonne National Laboratory used x-ray imagery to find for the first time that insects, although they do not have lungs, do not necessarily breathe completely passively, as had been believed previously; many insects rapidly compress and expand their trachea, head, and thorax in order to force air in and out of their bodies. One difference between x-raying a human and an insect is that if a medical x-ray machine was used on an insect, virtually 100% of the x-rays would pass through its body, and there would be no contrast in the image produced. Less penetrating x-rays of lower energies have to be used. For comparison, a typical human body mass is about 70 kg, whereas a typical ant is about 10 mg. Estimate the ratio of the thicknesses of tissue that must be penetrated by x-rays in one case compared to the other. `sqrt`
 25. Radio was first commercialized around 1920, and ever since then, radio signals from our planet have been spreading out across our galaxy. It is possible that alien civilizations could detect these signals and learn that there is life on earth. In the 90 years that the signals have been spreading at the speed of light, they have created a sphere with a radius of 90 light-years. To show an idea of the size of this sphere, I've indicated it in the figure as a tiny white circle on an image of a spiral galaxy seen edge on. (We don't have similar photos of our own Milky Way galaxy, because we can't see it from the outside.) So far we haven't received answering signals from aliens within this sphere, but as time goes on, the sphere will expand as suggested by the dashed outline, reaching more and more stars that might harbor extraterrestrial life. Approximately what year will it be when the sphere has expanded to fill a volume 100 times greater than the volume it fills today in 2010? `sqrt`
25. Radio was first commercialized around 1920, and ever since then, radio signals from our planet have been spreading out across our galaxy. It is possible that alien civilizations could detect these signals and learn that there is life on earth. In the 90 years that the signals have been spreading at the speed of light, they have created a sphere with a radius of 90 light-years. To show an idea of the size of this sphere, I've indicated it in the figure as a tiny white circle on an image of a spiral galaxy seen edge on. (We don't have similar photos of our own Milky Way galaxy, because we can't see it from the outside.) So far we haven't received answering signals from aliens within this sphere, but as time goes on, the sphere will expand as suggested by the dashed outline, reaching more and more stars that might harbor extraterrestrial life. Approximately what year will it be when the sphere has expanded to fill a volume 100 times greater than the volume it fills today in 2010? `sqrt`
26. Estimate the number of jellybeans in figure r on p. 56.
 27. At the grocery store you will see oranges packed neatly in stacks. Suppose we want to pack spheres as densely as possible, so that the greatest possible fraction of the space is filled by the spheres themselves, not by empty space. Let's call this fraction `f`. Mathematicians have proved that the best possible result is f ≈ 0.7405, which requires a systematic pattern of stacking. If you buy ball bearings or golf balls, however, the seller is probably not going to go to the trouble of stacking them neatly. Instead they will probably pour the balls into a box and vibrate the box vigorously for a while to make them settle. This results in a random packing. The closest random packing has f ≈ 0.64. Suppose that golf balls, with a standard diameter of 4.27 cm, are sold in bulk with the closest random packing. What is the diameter of the largest ball that could be sold in boxes of the same size, packed systematically, so that there would be the same number of balls per box? `sqrt`
27. At the grocery store you will see oranges packed neatly in stacks. Suppose we want to pack spheres as densely as possible, so that the greatest possible fraction of the space is filled by the spheres themselves, not by empty space. Let's call this fraction `f`. Mathematicians have proved that the best possible result is f ≈ 0.7405, which requires a systematic pattern of stacking. If you buy ball bearings or golf balls, however, the seller is probably not going to go to the trouble of stacking them neatly. Instead they will probably pour the balls into a box and vibrate the box vigorously for a while to make them settle. This results in a random packing. The closest random packing has f ≈ 0.64. Suppose that golf balls, with a standard diameter of 4.27 cm, are sold in bulk with the closest random packing. What is the diameter of the largest ball that could be sold in boxes of the same size, packed systematically, so that there would be the same number of balls per box? `sqrt`
28. Plutonium-239 is one of a small number of important long-lived forms of high-level radioactive nuclear waste. The world's waste stockpiles have about `10^3` metric tons of plutonium. Drinking water is considered safe by U.S. government standards if it contains less than `2×10^(-13) g"/"cm^3` of plutonium. The amount of radioactivity to which you were exposed by drinking such water on a daily basis would be very small compared to the natural background radiation that you are exposed to every year. Suppose that the world's inventory of plutonium-239 were ground up into an extremely fine dust and then dispersed over the world's oceans, thereby becoming mixed uniformly into the world's water supplies over time. Estimate the resulting concentration of plutonium, and compare with the government standard.
{Scaling applied to leaves}
Equipment:
leaves of three sizes, having roughly similar proportions of length, width, and thickness
balance
Each group will have one leaf, and should measure its surface area and volume, and determine its surface-to-volume ratio. For consistency, every group should use units of `cm^2`and `cm^3`, and should only find the area of one side of the leaf. The area can be found by tracing the area of the leaf on graph paper and counting squares. The volume can be found by weighing the leaf and assuming that its density is `1 g"/"cm^3` (the density of water). What implications do your results have for the plants' abilities to survive in different environments?
1.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.