12.2 Potential energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
12.2 Potential energy: energy of distance or closeness
We have already seen many examples of energy related to the distance between interacting objects. When two objects participate in an attractive noncontact force, energy is required to bring them farther apart. In both of the perpetual motion machines that started off the previous chapter, one of the types of energy involved was the energy associated with the distance between the balls and the earth, which attract each other gravitationally. In the perpetual motion machine with the magnet on the pedestal, there was also energy associated with the distance between the magnet and the iron ball, which were attracting each other.
The opposite happens with repulsive forces: two socks with the same type of static electric charge will repel each other, and cannot be pushed closer together without supplying energy.
In general, the term potential energy, with algebra symbol PE, is used for the energy associated with the distance between two objects that attract or repel each other via a force that depends on the distance between them. Forces that are not determined by distance do not have potential energy associated with them. For instance, the normal force acts only between objects that have zero distance between them, and depends on other factors besides the fact that the distance is zero. There is no potential energy associated with the normal force.
The following are some commonplace examples of potential energy:
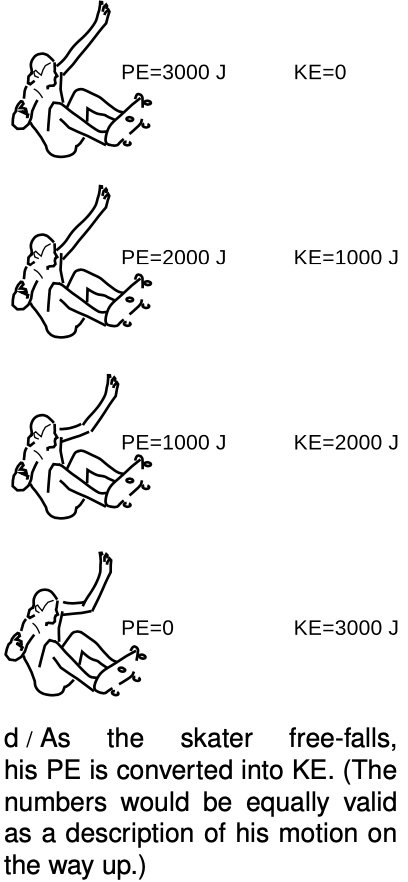
- gravitational potential energy: The skateboarder in the photo has risen from the bottom of the pool,
 converting kinetic energy into gravitational potential energy. After being at rest for an instant, he will go back down, converting PE back into KE.
converting kinetic energy into gravitational potential energy. After being at rest for an instant, he will go back down, converting PE back into KE. - magnetic potential energy: When a magnetic compass needle is allowed to rotate, the poles of the compass change their distances from the earth's north and south magnetic poles, converting magnetic potential energy into kinetic energy. (Eventually the kinetic energy is all changed into heat by friction, and the needle settles down in the position that minimizes its potential energy.)
- electrical potential energy: Socks coming out of the dryer cling together because of attractive electrical forces. Energy is required in order to separate them.
- potential energy of bending or stretching: The force between the two ends of a spring depends on the distance between them, i.e., on the length of the spring. If a car is pressed down on its shock absorbers and then released, the potential energy stored in the spring is transformed into kinetic and gravitational potential energy as the car bounces back up.
I have deliberately avoided introducing the term potential energy up until this point, because it tends to produce unfortunate connotations in the minds of students who have not yet been inoculated with a careful description of the construction of a numerical energy scale. Specifically, there is a tendency to generalize the term inappropriately to apply to any situation where there is the “potential” for something to happen: “I took a break from digging, but I had potential energy because I knew I'd be ready to work hard again in a few minutes.”
 An equation for gravitational potential energy
An equation for gravitational potential energy
All the vital points about potential energy can be made by focusing on the example of gravitational potential energy. For simplicity, we treat only vertical motion, and motion close to the surface of the earth, where the gravitational force is nearly constant. (The generalization to the three dimensions and varying forces is more easily accomplished using the concept of work, which is the subject of the next chapter.)
To find an equation for gravitational PE, we examine the case of free fall, in which energy is transformed between kinetic energy and gravitational PE. Whatever energy is lost in one form is gained in an equal amount in the other form, so using the notation `DeltaKE` to stand for `KE_f?KE_i` and a similar notation for PE, we have
`DeltaKE=-DeltaPE_(grav)`.
It will be convenient to refer to the object as falling, so that PE is being changed into KE, but the math applies equally well to an object slowing down on its way up. We know an equation for kinetic energy,
so if we can relate `v` to height, `y`, we will be able to relate `DeltaPE` to `y`, which would tell us what we want to know about potential energy. The `y` component of the velocity can be connected to the height via the constant acceleration equation
and Newton's second law provides the acceleration,
[Private Equation],
in terms of the gravitational force.
The algebra is simple because both equation [2] and equation [3] have velocity to the second power. Equation [2] can be solved for `v^2` to give `v^2=2KE"/"m`, and substituting this into equation [3], we find
`2(KE_f)/m=2(KE_i)/m+2aDeltay`.
Making use of equations [1] and [4] gives the simple result
[change in gravitational PE resulting from a change in height `Deltay`; `F` is the gravitational force on the object i.e., its weight; valid only near the surface of the earth, where `F` is constant]
Example 1: Dropping a rock
`=>` If you drop a 1-kg rock from a height of 1 m, how many joules of KE does it have on impact with the ground? (Assume that any energy transformed into heat by air friction is negligible.)
`=>` If we choose the `y` axis to point up, then `F_y` is negative, and equals `-(1 kg)(g)=-9.8 N`. A decrease in `y` is represented by a negative value of `Deltay`, `Deltay=-1 m`, so the change in potential energy is `-(-9.8 N)(-1 m)approx-10 J`. (The proof that newtons multiplied by meters give units of joules is left as a homework problem.) Conservation of energy says that the loss of this amount of PE must be accompanied by a corresponding increase in KE of 10 J.
It may be dismaying to note how many minus signs had to be handled correctly even in this relatively simple example: a total of four. Rather than depending on yourself to avoid any mistakes with signs, it is better to check whether the final result make sense physically. If it doesn't, just reverse the sign.
Although the equation for gravitational potential energy was derived by imagining a situation where it was transformed into kinetic energy, the equation can be used in any context, because all the types of energy are freely convertible into each other.
Example 2: Gravitational PE converted directly into heat
`=>` A 50-kg firefighter slides down a 5-m pole at constant velocity. How much heat is produced?
`=>` Since she slides down at constant velocity, there is no change in KE. Heat and gravitational PE are the only forms of energy that change. Ignoring plus and minus signs, the gravitational force on her body equals `mg`, and the amount of energy transformed is
`(mg)(5 m)=2500 J`.
On physical grounds, we know that there must have been an increase (positive change) in the heat energy in her hands and in the flagpole.
Here are some questions and answers about the interpretation of the equation `DeltaPE_(grav) = -F*Deltay` for gravitational potential energy.
Question: In a nutshell, why is there a minus sign in the equation?
Answer: It is because we increase the PE by moving the object in the opposite direction compared to the gravitational force.
Question: Why do we only get an equation for the change in potential energy? Don't I really want an equation for the potential energy itself?
Answer: No, you really don't. This relates to a basic fact about potential energy, which is that it is not a well defined quantity in the absolute sense. Only changes in potential energy are unambiguously defined. If you and I both observe a rock falling, and agree that it deposits 10 J of energy in the dirt when it hits, then we will be forced to agree that the 10 J of KE must have come from a loss of 10 joules of PE. But I might claim that it started with 37 J of PE and ended with 27, while you might swear just as truthfully that it had 109 J initially and 99 at the end. It is possible to pick some specific height as a reference level and say that the PE is zero there, but it's easier and safer just to work with changes in PE and avoid absolute PE altogether.
Question: You referred to potential energy as the energy that two objects have because of their distance from each other. If a rock falls, the object is the rock. Where's the other object?
Answer: Newton's third law guarantees that there will always be two objects. The other object is the planet earth.
Question: If the other object is the earth, are we talking about the distance from the rock to the center of the earth or the distance from the rock to the surface of the earth?
Answer: It doesn't matter. All that matters is the change in distance, `Deltay`, not `y`. Measuring from the earth's center or its surface are just two equally valid choices of a reference point for defining absolute PE.
Question: Which object contains the PE, the rock or the earth?
Answer: We may refer casually to the PE of the rock, but technically the PE is a relationship between the earth and the rock, and we should refer to the earth and the rock together as possessing the PE.
Question: How would this be any different for a force other than gravity?
Answer: It wouldn't. The result was derived under the assumption of constant force, but the result would be valid for any other situation where two objects interacted through a constant force. Gravity is unusual, however, in that the gravitational force on an object is so nearly constant under ordinary conditions. The magnetic force between a magnet and a refrigerator, on the other hand, changes drastically with distance. The math is a little more complex for a varying force, but the concepts are the same.
Question: Suppose a pencil is balanced on its tip and then falls over. The pencil is simultaneously changing its height and rotating, so the height change is different for different parts of the object. The bottom of the pencil doesn't lose any height at all. What do you do in this situation?
Answer: The general philosophy of energy is that an object's energy is found by adding up the energy of every little part of it. You could thus add up the changes in potential energy of all the little parts of the pencil to find the total change in potential energy. Luckily there's an easier way! The derivation of the equation for gravitational potential energy used Newton's second law, which deals with the acceleration of the object's center of mass (i.e., its balance point). If you just define `Deltay` as the height change of the center of mass, everything works out. A huge Ferris wheel can be rotated without putting in or taking out any PE, because its center of mass is staying at the same height.
self-check:
A ball thrown straight up will have the same speed on impact with the ground as a ball thrown straight down at the same speed. How can this be explained using potential energy?
(answer in the back of the PDF version of the book)
Discussion Question
A You throw a steel ball up in the air. How can you prove based on conservation of energy that it has the same speed when it falls back into your hand? What if you throw a feather up --- is energy not conserved in this case?
12.2 Potential energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.