0.12 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Selected Vocabulary
- matter — Anything that is affected by gravity.
- light — Anything that can travel from one place to another through empty space and can influence matter, but is not affected by gravity.
- operational definition — A definition that states what operations should be carried out to measure the thing being defined.
- Système International — A fancy name for the metric system.
- mks system — The use of metric units based on the meter, kilogram, and second. Example: meters per second is the mks unit of speed, not cm/s or km/hr.
- mass — A numerical measure of how difficult it is to change an object's motion.
- significant figures — Digits that contribute to the accuracy of a measurement.
Notation
- m — meter, the metric distance unit
- kg — kilogram, the metric unit of mass
- s — second, the metric unit of time
- M- — the metric prefix mega-, `10^6`
- k- — the metric prefix kilo-, `10^3`
- m- — the metric prefix milli-, `10^(-3)`
- `mu`- — the metric prefix micro-, `10^(-6)`
- `n`- — the metric prefix nano-, `10^(-9)`
Summary
Physics is the use of the scientific method to study the behavior of light and matter. The scientific method requires a cycle of theory and experiment, theories with both predictive and explanatory value, and reproducible experiments.
The metric system is a simple, consistent framework for measurement built out of the meter, the kilogram, and the second plus a set of prefixes denoting powers of ten. The most systematic method for doing conversions is shown in the following example:
`370 ms×(10^(-3) s)/(1 ms)=0.37 s`
Mass is a measure of the amount of a substance. Mass can be defined gravitationally, by comparing an object to a standard mass on a double-pan balance, or in terms of inertia, by comparing the effect of a force on an object to the effect of the same force on a standard mass. The two definitions are found experimentally to be proportional to each other to a high degree of precision, so we usually refer simply to “mass,” without bothering to specify which type.
A force is that which can change the motion of an object. The metric unit of force is the Newton, defined as the force required to accelerate a standard 1-kg mass from rest to a speed of 1 m/s in 1 s.
Scientific notation means, for example, writing `3.2×10^5` rather than `320000`.
Writing numbers with the correct number of significant figures correctly communicates how accurate they are. As a rule of thumb, the final result of a calculation is no more accurate than, and should have no more significant figures than, the least accurate piece of data.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Correct use of a calculator: (a) Calculate `(74658)/(53222+97554)` on a calculator. [Self-check: The most common mistake results in 97555.40.] `sqrt`
(b) Which would be more like the price of a TV, and which would be more like the price of a house, `$3.5×10^5` or `$3.55`?
2. Compute the following things. If they don't make sense because of units, say so.
(a) 3 cm + 5 cm
(b) 1.11 m + 22 cm
(c) 120 miles + 2.0 hours
(d) 120 miles / 2.0 hours
3. Your backyard has brick walls on both ends. You measure a distance of 23.4 m from the inside of one wall to the inside of the other. Each wall is 29.4 cm thick. How far is it from the outside of one wall to the outside of the other? Pay attention to significant figures.
4. The speed of light is `3.0×10^8 m"/"s`. Convert this to furlongs per fortnight. A furlong is 220 yards, and a fortnight is 14 days. An inch is 2.54 cm. `sqrt`
5. Express each of the following quantities in micrograms:
(a) 10 mg, (b) `10^4 g`, (c) 10 kg, (d) `100×10^3 g`, (e) 1000 ng. `sqrt`
6. (solution in the pdf version of the book) Convert 134 mg to units of kg, writing your answer in scientific notation.
7. In the last century, the average age of the onset of puberty for girls has decreased by several years. Urban folklore has it that this is because of hormones fed to beef cattle, but it is more likely to be because modern girls have more body fat on the average and possibly because of estrogen-mimicking chemicals in the environment from the breakdown of pesticides. A hamburger from a hormone-implanted steer has about 0.2 ng of estrogen (about double the amount of natural beef). A serving of peas contains about 300 ng of estrogen. An adult woman produces about 0.5 mg of estrogen per day (note the different unit!). (a) How many hamburgers would a girl have to eat in one day to consume as much estrogen as an adult woman's daily production? (b) How many servings of peas? `sqrt`
8. (solution in the pdf version of the book) The usual definition of the mean (average) of two numbers `a` and `b` is `(a+b)"/"2`. This is called the arithmetic mean. The geometric mean, however, is defined as `(ab)^(1/2)` (i.e., the square root of `ab`). For the sake of definiteness, let's say both numbers have units of mass. (a) Compute the arithmetic mean of two numbers that have units of grams. Then convert the numbers to units of kilograms and recompute their mean. Is the answer consistent? (b) Do the same for the geometric mean. (c) If `a` and `b` both have units of grams, what should we call the units of ab? Does your answer make sense when you take the square root? (d) Suppose someone proposes to you a third kind of mean, called the superduper mean, defined as `(ab)^(1/3)`. Is this reasonable?
9. In an article on the SARS epidemic, the May 7, 2003 New York Times discusses conflicting estimates of the disease's incubation period (the average time that elapses from infection to the first symptoms). “The study estimated it to be 6.4 days. But other statistical calculations ... showed that the incubation period could be as long as 14.22 days.” What's wrong here?
 10. The photo shows the corner of a bag of pretzels. What's wrong here?
10. The photo shows the corner of a bag of pretzels. What's wrong here?
11. The distance to the horizon is given by the expression `sqrt(2rh)`, where `r` is the radius of the Earth, and `h` is the observer's height above the Earth's surface. (This can be proved using the Pythagorean theorem.) Show that the units of this expression make sense. (See example 1 on p. 27 for an example of how to do this.) Don't try to prove the result, just check its units.
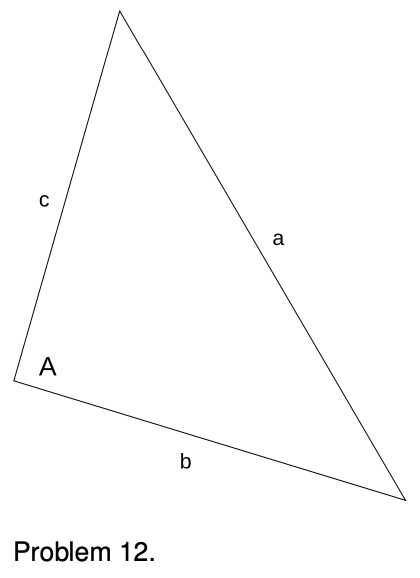 12. (solution in the pdf version of the book) (a) Based on the definitions of the sine, cosine, and tangent, what units must they have? (b) A cute formula from trigonometry lets you find any angle of a triangle if you know the lengths of its sides. Using the notation shown in the figure, and letting s=(a+b+c)/2 be half the perimeter, we have:
12. (solution in the pdf version of the book) (a) Based on the definitions of the sine, cosine, and tangent, what units must they have? (b) A cute formula from trigonometry lets you find any angle of a triangle if you know the lengths of its sides. Using the notation shown in the figure, and letting s=(a+b+c)/2 be half the perimeter, we have:
`tan A/2 = sqrt ( ( (s-b)(s-c) ) / (s(s-a)))`
Show that the units of this equation make sense. In other words, check that the units of the right-hand side are the same as your answer to part a of the question.
Exercise 0: Models and idealization
Equipment:
- coffee filters
- ramps (one per group)
- balls of various sizes
- sticky tape
- vacuum pump and “guinea and feather” apparatus (one)
The motion of falling objects has been recognized since ancient times as an important piece of physics, but the motion is inconveniently fast, so in our everyday experience it can be hard to tell exactly what objects are doing when they fall. In this exercise you will use several techniques to get around this problem and study the motion. Your goal is to construct a scientific model of falling. A model means an explanation that makes testable predictions. Often models contain simplifications or idealizations that make them easier to work with, even though they are not strictly realistic.
1. One method of making falling easier to observe is to use objects like feathers that we know from everyday experience will not fall as fast. You will use coffee filters, in stacks of various sizes, to test the following two hypotheses and see which one is true, or whether neither is true:
Hypothesis 1A: When an object is dropped, it rapidly speeds up to a certain natural falling speed, and then continues to fall at that speed. The falling speed is proportional to the object's weight. (A proportionality is not just a statement that if one thing gets bigger, the other does too. It says that if one becomes three times bigger, the other also gets three times bigger, etc.)
Hypothesis 1B: Different objects fall the same way, regardless of weight.
Test these hypotheses and discuss your results with your instructor.
2. A second way to slow down the action is to let a ball roll down a ramp. The steeper the ramp, the closer to free fall. Based on your experience in part 1, write a hypothesis about what will happen when you race a heavier ball against a lighter ball down the same ramp, starting them both from rest.
Hypothesis:..........................................................................................................
Show your hypothesis to your instructor, and then test it.
You have probably found that falling was more complicated than you thought! Is there more than one factor that affects the motion of a falling object? Can you imagine certain idealized situations that are simpler? Try to agree verbally with your group on an informal model of falling that can make predictions about the experiments described in parts 3 and 4.
3. You have three balls: a standard “comparison ball” of medium weight, a light ball, and a heavy ball. Suppose you stand on a chair and (a) drop the light ball side by side with the comparison ball, then (b) drop the heavy ball side by side with the comparison ball, then (c) join the light and heavy balls together with sticky tape and drop them side by side with the comparison ball.
Use your model to make a prediction:..........................................................................................................
Test your prediction.
4. Your instructor will pump nearly all the air out of a chamber containing a feather and a heavier object, then let them fall side by side in the chamber.
Use your model to make a prediction:..........................................................................................................
0.12 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.