The Radius of Perigee calculator computes is the distance between an object (often a planet) and orbiting body when the orbiting body is at perigee based on the semi-major axis (a) and the eccentricity (e) of the orbit.
INSTRUCTIONS: Choose units and enter the following:
- (a) Semi-major axis Orbital ellipse.
- (e) Eccentricity of Orbit (ellipse)
Radius of Perigee (rp): The calculator returns the radius of perigee in kilometers. However this can be automatically converted to other distance units including a full suite of astronomical distance units (e.g. light years, parsecs, astronomical units)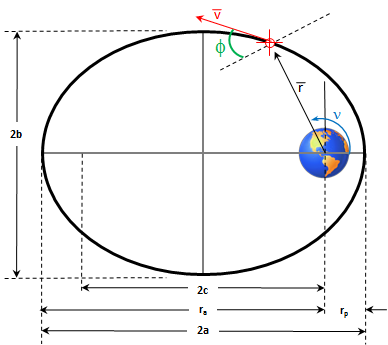 
diagram illustrating various orbital characteristics,
including radius of perigee rp
Related Calculators:
The Math / Science
The formula for the radius of perigee is:
rp = a•(1-e)
where:
- rp is the radius of perigee
- a is the semi-major axis
- e the eccentricity of the orbital ellipse
Perigee is the point in an orbit at which the orbiting body is closest to the object it orbits. Thus, the Radius of Perigee represents the minimum distance between an orbiting body and the object it orbits. Radius of Perigee may be contrasted to Radius of Apogee, which is the maximum distance between orbiting and orbited bodies.
This equation produces the Radius of Perigee rp, based on length of semi-major axis (a) and eccentricity (e) of orbit. Distances are measured from the centers of bodies.
Example Parameters
| Orbit | Semi major axis | Eccentricity |
|---|---|---|
| Earth (about Sun)1 | 149.60 x 106 km | 0.0167 |
| Moon (about Earth)2 | 0.3844 x 106 km | 0.0549 |
| Saturn (about Sun)3 | 1,433.53 x 106 km | 0.0565 |
Remembering the Difference between Perigee and Apogee
Since apogee and perigee are not commonly used terms, they are often confused. A simple memory convention to remember the difference is this, count the number of letters. Apo and far, have three letters. Peri and near have four letters. Therefore perigee is the nearest point in the orbit, and apogee is the farthest point in the orbit.
History
The understanding of orbital perigee arose directly from Kepler's laws of planetary motion published in 16094.