The Radius of Apogee calculator computes is the distance between an object (often a planet) and orbiting body when the orbiting body is at apogee based on the semi-minor axis (a) and the eccentricity (e) of the orbit.
INSTRUCTIONS: Choose the preferred distance units and enter the following:
Radius of Apogee (ra): The calculator returns the radius of apogee in kilometers. However this can be automatically converted to other distance units including a full suite of astronomical distance units (e.g. light years, parsecs, astronomical units)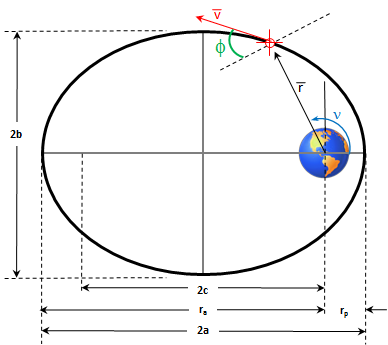 
diagram illustrating various orbital characteristics,
including radius of apogee ra
The Math / Science
The formula for the radius of apogee is:
ra = a•(1+e)
where:
- ra is the radius of apogee
- a is the semi-major axis
- e the eccentricity of the orbital ellipse
Apogee is the point in an orbit at which the orbiting body is furthest to the object it orbits. Thus, the Radius of Apogee represents the maximum distance between an orbiting body and the object it orbits. Radius of Apogee may be contrasted to Radius of Perigee, which is the minimum distance between orbiting and orbited bodies.
This equation produces the Radius of Apogee ra, based on length of semi-minor axis (a) and eccentricity (e) of an elliptical orbit. Distances are measured from the centers of bodies.
Example Parameters
| Orbit | Semi major axis | Eccentricity |
|---|---|---|
| Earth (about Sun)1 | 149.60 x 106 km | 0.0167 |
| Moon (about Earth)2 | 0.3844 x 106 km | 0.0549 |
| Saturn (about Sun)3 | 1,433.53 x 106 km | 0.0565 |
Remembering the Difference between Perigee and Apogee
Since apogee and perigee are not commonly used terms, they are often confused. A simple memory convention to remember the difference is this, count the number of letters. Apo and far, have three letters. Peri and near have four letters. Therefore perigee is the nearest point in the orbit, and apogee is the farthest point in the orbit.
History
The understanding of orbital perigee arose directly from Kepler's laws of planetary motion published in 16094.
- ^ http://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html
- ^ http://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html
- ^ http://nssdc.gsfc.nasa.gov/planetary/factsheet/saturnfact.html
- ^ http://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion