The Volume of the Frustum of a Right Squared-base Pyramid 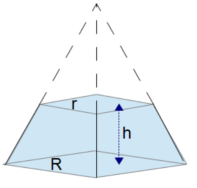calculator computes the volume of a right square based pyramid with a frustum defined by base side length (R) and top side length (r) and height (h) in between.

INSTRUCTIONS:  Choose units and enter the following:

• (r)   Length of one side of the four-sided square top (see diagram).
• (R)  Length of one side of the four-sided square base (see diagram).
• (h)  Height of frustum.  This is the distance between the base and the top.

Pyramid Frustum Volume (V): The volume is returned in cubic meters.  However, the user can automatically convert this to any of the other volume units (e.g. cubic feet, liters, or gallons) via the pull-down menu.

The Math / Science

A Right Square Pyramid has a four sided base where all four sides are equal and have equal angled corners (90^o), which is a square.  The pyramid is a right pyramid if the apex of the pyramid is directly above the center of the base square. The formula for the volume of a pyramid with a triangle base is:

     `V = 1/3 * h*(R^2+R * r+r^2)`  

where:

• V = volume of square pyramid frustum
• h = height of pyramid
• r = side length of top
• R = side length of base

Pyramid Calculators

• Pyramid Geometries
• Volume of a Pyramid
• Mass or Weight of a Pyramid 
• Volume of a Frustum of a Pyramid
• Mass of a Frustum of a Pyramid
• Volume of a Polygon Based Pyramid
• Mass of a Polygon Based Pyramid
• Volume of a Frustum of a Polygon Based Pyramid
• Mass of a Frustum of a Polygon Based Pyramid

A regular pyramid is a type of pyramid that has the following characteristics:

1. Base: The base of a regular pyramid is a regular polygon, meaning all sides of the polygon are equal in length, and all interior angles are equal. Examples of regular polygons include equilateral triangles, squares, and regular pentagons.
2. Apex: The apex is the point directly above the center of the base. In a regular pyramid, the apex is aligned such that the line segment (height) from the apex to the center of the base is perpendicular to the base.
3. Lateral Faces: The lateral faces of the pyramid are congruent isosceles triangles. Each triangle shares a side with the base of the pyramid and meets at the apex.
4. Height: The height of the pyramid is the perpendicular distance from the apex to the center of the base.

Because of these properties, a regular pyramid is symmetric around its vertical axis (the line connecting the apex to the center of the base).