Interest Rate - Annual

The Annual Interest Rate calculator computes the annual interest rate for a fixed rate loan.

INSTRUCTIONS: Choose the preferred currency units and enter the following:

• (P)  This is the original principal of the loan
• (N)  This is the duration of the loan
• (Pmt)  This is the monthly payment amount

Annual Interest Rate:  The calculator return the annual % interest rate.  

Related Calculators:

• Monthly Interest Rate: : This computes the monthly interest rate on a fixed rate loan based on the monthly payment, duraton of the loan and principal amount.
• Monthly Payment: : This computes the monthly payment on a fixed rate loan based on the annual interest rate, duraton of the loan and principal amount.

The  Math / Science

A loan which has a fixed interest rate, r, and N equal monthly payments of the amount, Paymnt, can be characterized by the equation:

     `P*r = "Paymnt" * ( 1 - 1/(1+r)^N  )`

Rearranging we can define:   `f(r) = P/"Paymnt" *r +1/(1+r)^N  - 1`

Setting  `f(r) = 0` to find the roots of this function, we can now use the iterative Newton Raphson Method to find the annual interest rate, r.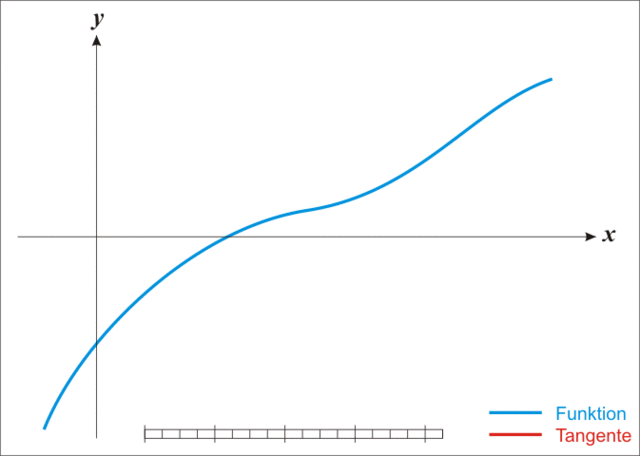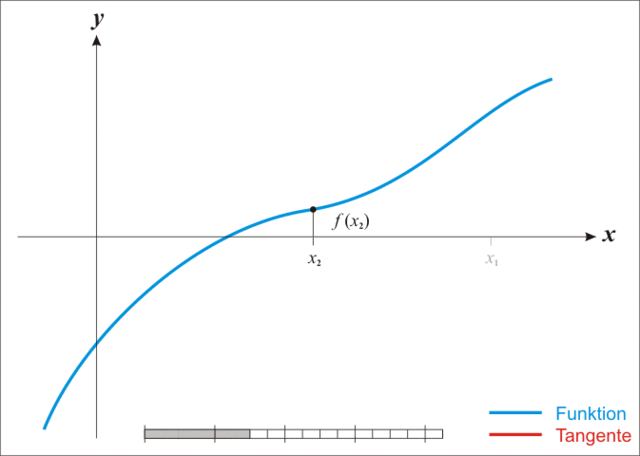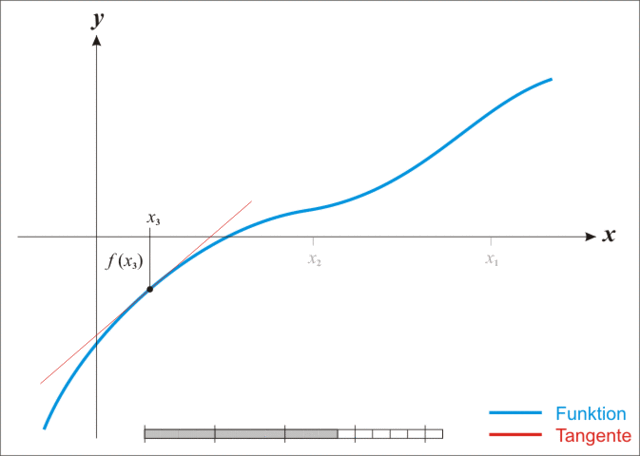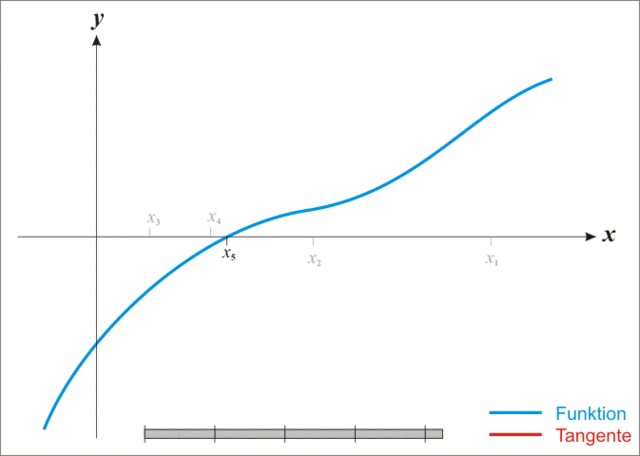  
Newtonian Iteration Animation, Wikipedia / Ralph Pfeifer
_{CC BY-3.0} 

Newton Raphson Method¹

The Newton Raphson Method is an iterative numerical analysis method for finding the roots of a real-value function.  We want to find in this case the interest rate, r, that is where `f(r) = 0`.

The Newton Raphson Method makes successively better approximations of the value of r by using the derivative of `f(r)`, which we denote `f'(r)`, to define the tangent at the point `[r_n, f(r_n)]`.  Each successive approximation uses the tangent thus derived for `r_n`, which will intersect the x-axis at the next value `r_(n+1)`.

If we pick a first guess interest rate, `r_0`, the Newton Raphson Method tells us that a next better approximation is given as follows:

`r_1 = r_0 - f(r_0) / (f'(r_0))`

If we look at the example graph at the right of the function, `f(x)`,  the x-value approximation where the function crosses the x-axis at `x_1` is the intersection with the x-axis of the tangent to the graph which touches the curve `f(x)` at the point `(x_0, f (x_0))`.

The Newton Raphson Method generalizes the successive better approximations of the function's root (where the function intersects the x-axis) with the following equation:

`x_(n+1) = x_n - f(x_n) / (f'(x_n))`   This equation iterates over some number of successive approximations of `x_(n+1)` and arrives quickly at a very close approximation of the interest rate, `r_(n+1)`.

1. ^ http://en.wikipedia.org/wiki/Newton%27s_method