The Distance to the Horizon at Altitude calculator computes the distance to the horizon taking into account the altitude of the observer, the altitude at the horizon and the mean Equatorial Radius of the Earth.
INSTRUCTIONS: Choose units and enter the following:
- (AO) Altitude of Observer
- (AH) Altitude at Horizon
Distance (D): The calculator returns the distance in meters. However this can be automatically converted to other distance units (e.g. miles, nautical miles or kilometers) via the pull-down menu.
The Math / Science
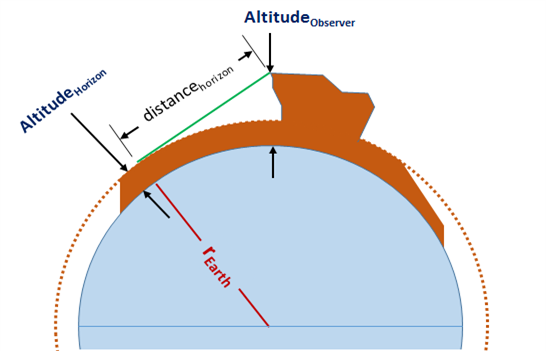
This equation provides an approximation for the distance you can see to the horizon. This equation uses the Tangent-Secant Theorem to approximate the distance to a tangent point -- the horizon -- on the Earth's surface, given that you know the approximate elevation near the horizon and that you know your observation elevation.
Input to this equation:
- `"Altitude"_"Observer"` = the altitude above sea level at which you're viewing a point at the horizon
- `"Altitude"_"Horizon"` = the altitude above sea level at a location near the horizon
Output of this equation:
- `"Distance"_"horizon"` = approximate distance to a point on the horizon
Notes
Equation as an Approximation
This equation is an approximation because, for one thing, the Earth is not a perfect sphere. Also, this is likely to be used where you are not looking at the horizon at sea level. But if we think of the Earth as a perfect sphere for this approximation and use one of our multiple vCalc values from the Constants taxonomy for the Earth's radius -- Yes, Flat Earth Society, the Earth is quite definitely round -- we can do a good approximation for the distance we can see at various elevations to the horizon.
I'm going to use the WGS-84 estimate of the Earth equatorial radius for these purposes, just because it is a well-known value for the Earth's radius.
This equation approximates the distance to the horizon, assuming the following among many things:
- the Earth is spherical
- the WGS-84 equatorial radius is a good approximation for a spherical Earth model's radius
- we neglect any affect the atmosphere may have on our seeing a point that far in the distance
- our viewing location is higher than the point we're viewing on the horizon
If we can accept all these assumptions, our approximation can be based on a very simple application of the Tangent-Secant Theorem.
For a version of this calculation which is based only on the altitude separation of the observer and the horizon, see Distance to the sea Level Horizon.
Derivation of the Equation
The Tangent-Secant Theorem tells us that the distance from a point outside a circle is given by `d = sqrt(h* (h+2r))`, where h is the distance of the point outside the circle and r is the radius of the circle.
If we assume the circle is the imaginary concentric sphere around the Earth at the elevation near the horizon and the point is our observation point looking toward the horizon, we can use the Tangent-Secant Theorem to compute an approximate distance between us as the observer and the horizon. We make the radius of the circle equivalent to the radius the altitude near the horizon and our point outside the circle the difference between our altitude and the horizon altitude.
An example:
Living in Colorado, where there are large open spaces unencumbered by trees (although mountains do seem to get in the way) and having just returned from a trip to the four corners area near Durango, CO, I was wondering if I had been looking into New Mexico when I was looking to the horizon from atop Mesa Verde. The view to the south looks far past the San Juan River but I was wondering if I was seeing as far as New Mexico.
This works most accurately for looking at the ocean horizon from some vantage point higher than the shoreline but we'll derive the equation here so that you can use it also as an approximation for elevations above the local (spherical) plane of the Earth. That way I can make an approximation for looking at the horizon from Mesa Verde, looking far south at what was probably a New Mexico horizon.
If I take the approximate elevation at the San Juan River to the south of Mesa Verde (around 4,600 feet) as my elevation at the horizon and I take my altitude on Mesa Verde (around 8,400 feet) as the elevation at my observation location, this equation's approximation tells me I can see a distance in the neighborhood of 75.5 miles (121.5 km). That is easily enough to be seeing into New Mexico. Even if this is a rough approximation, I know I am looking beyond the Colorado border.
Try this in central Wyoming too, where there are many places you can look all the way to the horizon in every direction -- 360 degrees around -- and not see a house, a power line or any vestige of human habitation. There you can truly see to the horizon in the crisp dry summer air.