15.4 Torque: the rate of transfer of angular momentum by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
15.4 Torque: the rate of transfer of angular momentum
Force can be interpreted as the rate of transfer of momentum. The equivalent in the case of angular momentum is called torque (rhymes with “fork”). Where force tells us how hard we are pushing or pulling on something, torque indicates how hard we are twisting on it. Torque is represented by the Greek letter tau, `tau`, and the rate of change of an object's angular momentum equals the total torque acting on it,
`tau_"total"=(DeltaL)/(Deltat)`.
(If the angular momentum does not change at a constant rate, the total torque equals the slope of the tangent line on a graph of `L` versus `t`.)
 As with force and momentum, it often happens that angular momentum recedes into the background and we focus our interest on the torques. The torque-focused point of view is exemplified by the fact that many scientifically untrained but mechanically apt people know all about torque, but none of them have heard of angular momentum. Car enthusiasts eagerly compare engines' torques, and there is a tool called a torque wrench which allows one to apply a desired amount of torque to a screw and avoid over tightening it.
As with force and momentum, it often happens that angular momentum recedes into the background and we focus our interest on the torques. The torque-focused point of view is exemplified by the fact that many scientifically untrained but mechanically apt people know all about torque, but none of them have heard of angular momentum. Car enthusiasts eagerly compare engines' torques, and there is a tool called a torque wrench which allows one to apply a desired amount of torque to a screw and avoid over tightening it.
Torque distinguished from force
Of course a force is necessary in order to create a torque - you can't twist a screw without pushing on the wrench - but force and torque are two different things. One distinction between them is direction. We use positive and negative signs to represent forces in the two possible directions along a line. The direction of a torque, however, is clockwise or counterclockwise, not a linear direction.
The other difference between torque and force is a matter of leverage. A given force applied at a door's knob will change the door's angular momentum twice as rapidly as the same force applied halfway between the knob and the hinge. The same amount of force produces different amounts of torque in these two cases.
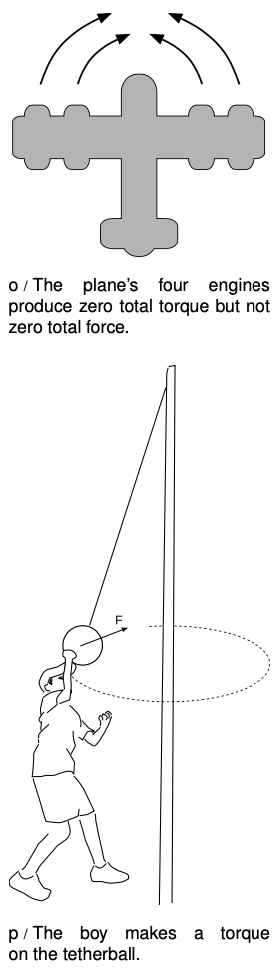 It is possible to have a zero total torque with a nonzero total force. An airplane with four jet engines, o, would be designed so that their forces are balanced on the left and right. Their forces are all in the same direction, but the clockwise torques of two of the engines are canceled by the counterclockwise torques of the other two, giving zero total torque.
It is possible to have a zero total torque with a nonzero total force. An airplane with four jet engines, o, would be designed so that their forces are balanced on the left and right. Their forces are all in the same direction, but the clockwise torques of two of the engines are canceled by the counterclockwise torques of the other two, giving zero total torque.
Conversely we can have zero total force and nonzero total torque. A merry-go-round's engine needs to supply a nonzero torque on it to bring it up to speed, but there is zero total force on it. If there was not zero total force on it, its center of mass would accelerate!
Relationship between force and torque
How do we calculate the amount of torque produced by a given force? Since it depends on leverage, we should expect it to depend on the distance between the axis and the point of application of the force. We'll derive an equation relating torque to force for a particular very simple situation, and state without proof that the equation actually applies to all situations.
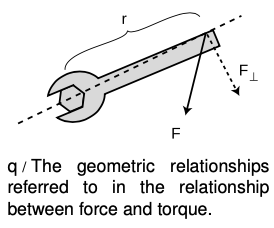
To try to pin down this relationship more precisely, let's imagine hitting a tetherball, figure p. The boy applies a force `F` to the ball for a short time `Deltat`, accelerating the ball from rest to a velocity `v`. Since force is the rate of transfer of momentum, we have `F` Since the initial velocity is zero, `Deltav` is the same as the final velocity `v`. Multiplying both sides by `r` gives `F=(mDeltav)/(Deltat)`
`F_r=(mvr)/(Deltat)`.
But `mvr` is simply the amount of angular momentum he's given the ball, so `mvr"/"Deltat` also equals the amount of torque he applied. The result of this example is
`tau=Fr`
Figure p was drawn so that the force `F` was in the direction tangent to the circle, i.e., perpendicular to the radius `r`. If the boy had applied a force parallel to the radius line, either directly inward or outward, then the ball would not have picked up any clockwise or counterclockwise angular momentum.
If a force acts at an angle other than 0 or 90° with respect to the line joining the object and the axis, it would be only the component of the force perpendicular to the line that would produce a torque,
`tau=F_(bot)r`
Although this result was proved under a simplified set of circumstances, it is more generally valid:
relationship between force and torque
 The rate at which a force transfers angular momentum to an object, i.e., the torque produced by the force, is given by
The rate at which a force transfers angular momentum to an object, i.e., the torque produced by the force, is given by
`|tau|=r|F_(bot)|`,
where `r` is the distance from the axis to the point of application of the force, and `F_(bot)` is the component of the force that is perpendicular to the line joining the axis to the point of application.
The equation is stated with absolute value signs because the positive and negative signs of force and torque indicate different things, so there is no useful relationship between them. The sign of the torque must be found by physical inspection of the case at hand.
From the equation, we see that the units of torque can be written as newtons multiplied by meters. Metric torque wrenches are calibrated in `N*m`, but American ones use foot-pounds, which is also a unit of distance multiplied by a unit of force. We know from our study of mechanical work that newtons multiplied by meters equal joules, but torque is a completely different quantity from work, and nobody writes torques with units of joules, even though it would be technically correct.
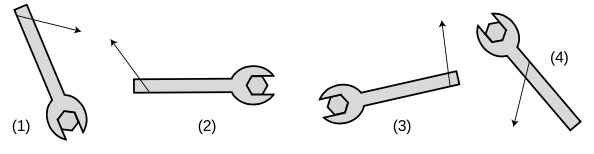
Compare the magnitudes and signs of the four torques shown in the figure.
Example 9: How torque depends on the direction of the force
`=>` How can the torque applied to the wrench in the figure be expressed in terms of `r`, `|F|`, and the angle `theta` between these two vectors?
`=>` The force vector and its `F_(tau)` component form the hypotenuse and one leg of a right triangle,
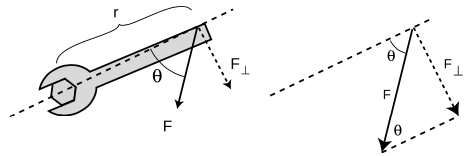
and the interior angle opposite to `F_9(bot)` equals `theta`. The absolute value of `F_(bot)` can thus be expressed as
`F_(bot)=|F|sintheta`,
leading to
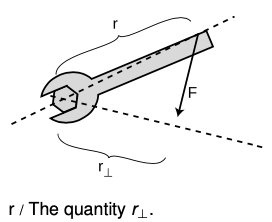 Sometimes torque can be more neatly visualized in terms of the quantity `r(tau)` shown in figure r, which gives us a third way of expressing the relationship between torque and force:
Sometimes torque can be more neatly visualized in terms of the quantity `r(tau)` shown in figure r, which gives us a third way of expressing the relationship between torque and force:
`|tau|=r_(bot)|F|`.
Of course you would not want to go and memorize all three equations for torque. Starting from any one of them you could easily derive the other two using trigonometry. Familiarizing yourself with them can however clue you in to easier avenues of attack on certain problems.
The torque due to gravity
 Up until now we've been thinking in terms of a force that acts at a single point on an object, such as the force of your hand on the wrench. This is of course an approximation, and for an extremely realistic calculation of your hand's torque on the wrench you might need to add up the torques exerted by each square millimeter where your skin touches the wrench. This is seldom necessary. But in the case of a gravitational force, there is never any single point at which the force is applied. Our planet is exerting a separate tug on every brick in the Leaning Tower of Pisa, and the total gravitational torque on the tower is the sum of the torques contributed by all the little forces. Luckily there is a trick that allows us to avoid such a massive calculation. It turns out that for purposes of computing the total gravitational torque on an object, you can get the right answer by just pretending that the whole gravitational force acts at the object's center of mass.
Up until now we've been thinking in terms of a force that acts at a single point on an object, such as the force of your hand on the wrench. This is of course an approximation, and for an extremely realistic calculation of your hand's torque on the wrench you might need to add up the torques exerted by each square millimeter where your skin touches the wrench. This is seldom necessary. But in the case of a gravitational force, there is never any single point at which the force is applied. Our planet is exerting a separate tug on every brick in the Leaning Tower of Pisa, and the total gravitational torque on the tower is the sum of the torques contributed by all the little forces. Luckily there is a trick that allows us to avoid such a massive calculation. It turns out that for purposes of computing the total gravitational torque on an object, you can get the right answer by just pretending that the whole gravitational force acts at the object's center of mass.
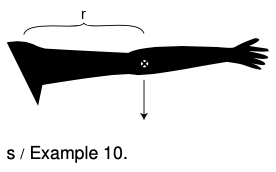
Example 10: Gravitational torque on an outstretched arm
`=>` Your arm has a mass of 3.0 kg, and its center of mass is 30 cm from your shoulder. What is the gravitational torque on your arm when it is stretched out horizontally to one side, taking the shoulder to be the axis?
`=>` The total gravitational force acting on your arm is
`|F|=(3.0 kg)(9.8 m"/"s^2)=29 N`.
For the purpose of calculating the gravitational torque, we can treat the force as if it acted at the arm's center of mass. The force is straight down, which is perpendicular to the line connecting the shoulder to the center of mass, so
`F_(bot)=|F|=29 N`.
Continuing to pretend that the force acts at the center of the arm, `r` equals 30 cm = 0.30 m, so the torque is
`tau=rF_(bot)=9 N*m`.
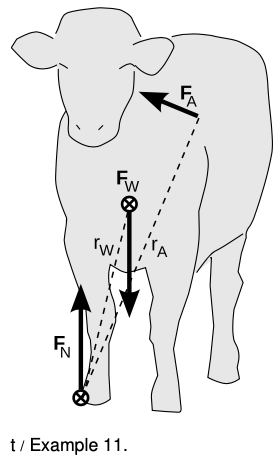 Example 11: Cow tipping
Example 11: Cow tipping
In 2005, Dr. Margo Lillie and her graduate student Tracy Boechler published a study claiming to debunk cow tipping. Their claim was based on an analysis of the torques that would be required to tip a cow, which showed that one person wouldn't be able to make enough torque to do it. A lively discussion ensued on the popular web site slashdot.org (“news for nerds, stuff that matters”) concerning the validity of the study. Personally, I had always assumed that cow-tipping was a group sport anyway, but as a physicist, I also had some quibbles with their calculation. Here's my own analysis.
There are three forces on the cow: the force of gravity `F_W`, the ground's normal force `F_N`, and the tippers' force `F_A`.
As soon as the cow's left hooves (on the right from our point of view) break contact with the ground, the ground's force is being applied only to hooves on the other side. We don't know the ground's force, and we don't want to find it. Therefore we take the axis to be at its point of application, so that its torque is zero.
For the purpose of computing torques, we can pretend that gravity acts at the cow's center of mass, which I've placed a little lower than the center of its torso, since its legs and head also have some mass, and the legs are more massive than the head and stick out farther, so they lower the c.m. more than the head raises it. The angle `theta_W` between the vertical gravitational force and the line `r_W` is about `14°`. (An estimate by Matt Semke at the University of Nebraska-Lincoln gives `20°`, which is in the same ballpark.)
To generate the maximum possible torque with the least possible force, the tippers want to push at a point as far as possible from the axis, which will be the shoulder on the other side, and they want to push at a 90 degree angle with respect to the radius line `r_A`.
When the tippers are just barely applying enough force to raise the cow's hooves on one side, the total torque has to be just slightly more than zero. (In reality, they want to push a lot harder than this - hard enough to impart a lot of angular momentum to the cow fair in a short time, before it gets mad and hurts them. We're just trying to calculate the bare minimum force they can possibly use, which is the question that science can answer.) Setting the total torque equal to zero,
`tau_N+tau_W+tau_A=0`,
and letting counterclockwise torques be positive, we have
`0-mgr_Wsintheta_W+F_Ar_Asin90°=0`
`F_A=r_W/r_Amgsintheta_W`
`approx1/1.5(680 kg)(9.8 m"/"s^2)sin14°`
`=1100 N`.
The 680 kg figure for the typical mass of a cow is due to Lillie and Boechler, who are veterinarians, so I assume it's fairly accurate. My estimate of 1100 N comes out significantly lower than their 1400 N figure, mainly because their incorrect placement of the center of mass gives `theta_W=24°`. I don't think 1100 N is an impossible amount of force to require of one big, strong person (it's equivalent to lifting about 110 kg, or 240 pounds), but given that the tippers need to impart a large angular momentum fairly quickly, it's probably true that several people would be required.
The main practical issue with cow tipping is that cows generally sleep lying down. Falling on its side can also seriously injure a cow.
Discussion Questions
A This series of discussion questions deals with past students' incorrect reasoning about the following problem.
Suppose a comet is at the point in its orbit shown in the figure. The only force on the comet is the sun's gravitational force.
Throughout the question, define all torques and angular momenta using the sun as the axis.
(1) Is the sun producing a nonzero torque on the comet? Explain.
 (2) Is the comet's angular momentum increasing, decreasing, or staying the same? Explain.
(2) Is the comet's angular momentum increasing, decreasing, or staying the same? Explain.
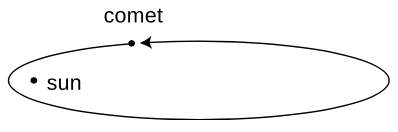
Explain what is wrong with the following answers. In some cases, the answer is correct, but the reasoning leading up to it is wrong.
(a) Incorrect answer to part (1): “Yes, because the sun is exerting a force on the comet, and the comet is a certain distance from the sun.”
(b) Incorrect answer to part (1): “No, because the torques cancel out.”
(c) Incorrect answer to part (2): “Increasing, because the comet is speeding up.”
B Which claw hammer would make it easier to get the nail out of the wood if the same force was applied in the same direction?
C You whirl a rock over your head on the end of a string, and gradually pull in the string, eventually cutting the radius in half. What happens to the rock's angular momentum? What changes occur in its speed, the time required for one revolution, and its acceleration? Why might the string break?
D A helicopter has, in addition to the huge fan blades on top, a smaller propeller mounted on the tail that rotates in a vertical plane. Why?
E The photo shows an amusement park ride whose two cars rotate in opposite directions. Why is this a good design?
15.4 Torque: the rate of transfer of angular momentum
by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.