The Rock Climbing Fall Impact Force equation computes 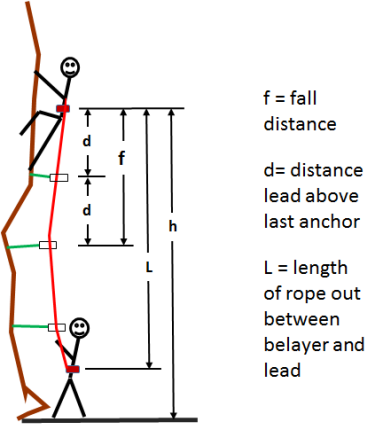 the Impact force of a fall on a climbing rope.
the Impact force of a fall on a climbing rope.
INSTRUCTIONS: Choose units and enter the following:
- (d) Lead climber's distance above last anchor point.
- (m) Climber's mass, thus the mass creating the impact force on the rope
- (k) Elasticity constant for the rope (in choice of system of measurement).
Impact Force (IF): The calculator returns the impact force in Newtons. However this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The force of impact is calculated as the force on an undampened harmonic oscillator (the rope is like a spring), which has an elasticity factor, k, that is uniquely attributed to each rope. You must choose the units of the rope's elasticity factor (spring factor) as SI (N/m) or US (lbf/ft). See the NOTES Page for a complete derivation of this equation.
* Note fall distance is twice d
IMPACT FORCE AND CLIMBING ROPES
Modern rock climbing ropes have been designed to absorb a large portion of a fall, lessening the potential that the force of arresting a fall could cause the falling climber injury. Modern ropes have an ability to stretch and some of the energy of the fall is actually converted to thermal energy, so it is important to know how many falls of high energy have been taken on a rope, as the core fibers can be damaged by heat in severe falls.
This equation is an idealized representation of the Impact Force of a weight falling a distance and being arrested by a spring-like opposing force. This is an approximation of the scenario depicted here of a lead climber falling some distance while on belay. The actual combination of forces that would come into play in such a fall scenario include many other factors such as, but not limited to the following:
- The rope passes over a carabiner attached to the last anchor below the climber. There is a friction force at that turning point of the rope that can be included in the assessment of Impact Force experienced by the falling climber.
- The lead climber's momentum in many cases is not perfectly vertical and thus has a force component that is not aligned with the force of gravity
- The rope that is stretching continues beyond the anchor point and continues back down to the belayer, So the length of rope that can stretch as a spring-like element is the length the climber falls plus the length between the belayer and the anchor point. The maximum tension in the rope on the belayer's side of the anchor point may be less than the tension on the falling climber's side of the anchor point due to the friction at the anchor point among other factors
- The rope leading from belayer to anchor point may not be straight, having passed through potentially numerous carabiners attached to anchors above the belayer and experiencing frictional drag at points where the rope's path turns.
- The lead climber's climbing harness may absorb some force of the fall.
- The belayer's harness and belay device may absorb some force from the fall, in most cases probably a minimal amount.
- Not lease of the factors contributing to the distribution of forces across many attenuating elements is the separation distance between the belayer and his anchor. Typically there is some slack between the belayer and his base anchor so that with a fall the motion of the belayer themself absorbs some force.
The derivation of the formula for the Impact Force on a lead climber of mass, m, falling a distance of twice the distance, d, to the last anchor.
1. Potential energy of lead climber at height h, `P_h = m*g* h`
2. Potential energy of the rope "spring" as it absorbs fall, `P_"spring" = (1/2) k*x^2 - m*g*x`,
where `x` is the stretch of the rope generating some force against the falling body at the point the rope begins to arrest the climbers fall.
Because of conservation of energy, these two potential energies are equal (`P_h = P_"spring"`) at the point of maximum tension in the rope, which gives:
3. `m*g*2d` = ` (1/2) k*x^2 - m*g*x`
Reforming the equation gives us `(1/2*k) * x^2 - (m*g)*x - m*g*2d = 0`
Solving the quadratic equation for x using a = `1/2*k`; b = -m*g ; c = `-m*g*2d`
4. x = `-(-mg) +- sqrt((mg)^2 - 4* (1/2* k) * (-m*g*2d) )/(2*(1/2*k))`
Simplifying we get:
5. x = `(mg + sqrt( (mg)^2 + 2*k * m *g*2d))/k`
Then substituting this representation of x into the formula `F_"Max Tension" = k*x`, which cancels the k term in the denominator of the expression for x, we get the formula for the Impact Force of the lead climber falling:
6. `F_"Max Tension" = k * x = mg + sqrt( (mg)^2 + 4*k * m *g*d)`