The Rotational Speed at Latitude calculator computes the rotational speed on the surface of the Earth based on the Earth's Rotation Rate and the latitude.
INSTRUCTIONS: Enter the following:
- (α) Latitude (Latitude goes from 0 degrees at the equator to 90 degrees at either the North Pole or the South Pole).
Rotational Speed (S): The calculator returns the Rotational Speed in miles per hour. However, this can be automatically converted to other velocity units (e.g. meters per second or kilometers per hour).
Note: to convert from Degrees, Minutes and Seconds to Decimal Degrees, CLICK HERE.
The Math / Science
The rotation rate of the Earth is constant. However, one's distance from the polar axis is a function of latitude. Based on one's latitude, the rotational speed can be computed. Note: latitude can be either north or south, but the effect on the rotational speed is the same. The formula for the Rotational Speed at Latitude is:
where:
- s is the rotational speed at a latitude on Earth
- Re is the equatorial radius of the Earth
- α is the latitude
- Sd is the duration of a sidereal day
How fast are you really moving?
This equation computes the rotational speed (S) of a point on the Earth defined by its latitude (`alpha`). This equation assumes a round Earth approximation and uses the WGS-84 value for the .
 DERIVATION
DERIVATION
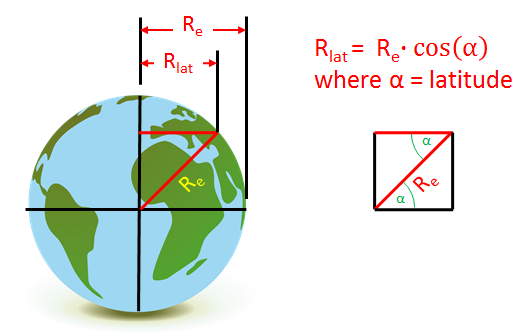
First we recognize the circle that is the equator and the circle created by the rotation of a point on the Earth at a non-zero latitude describe circles in parallel planes. Thus the radius of that circle at a specified latitude and the radius at the equator can be rotated in those parallel planes to be parallel lines -- as drawn in the figure at the left. The black line at the equator is parallel to the red radius of dimension Rlat.
These two radii crossed by the radius drawn diagonal from the center of the Earth to the specified latitude, form two internal opposite angles, `alpha`. We know from basic geometry that the two internal angles (`alpha`) in the figure are equal. The top red line of the triangle is then the cosine of the angle, `alpha`, multiplied by the length of the right triangle's hypotenuse:
Rlat = Re•cos(α) where Re is 6378137.0 m
Next, knowing the circumference of the circle whose radius is Rlat is given by Circumference = 2•π•Rlat we have the distance a point rotates each day at the latitude given by `alpha`.
Then we can compute the instantaneous velocity of a point on the globe at the specified latitude, α, by dividing the distance traveled in one day (in one rotation of the globe) by the number of hours in a sidereal day ( 23.9344699 hours). A sidereal day is the true period of a 360 degree rotation of the Earth in space. This takes into account the difference in from solar day attributed to the Earth's flight around the Sun.
Examples
- If we enter the latitude of Columbus, Ohio (39.961176 degrees) -- home to THE Ohio State University -- we find the rotational speed of the horseshoe stadium is approximately 795.3 mph. So, when a Buckeye fan is shouting O - H, their seat is moving at a pretty good speed.
- If we enter the latitude 0 degrees to determine the rotational speed at the equator, we find the rotational speed of a point at the equator is approximately 1037.6 mph.
- If we enter the latitude of London England (about 51.533 degrees), we find the rotational speed of the London Bridge is approximately 645.4 mph.
- If we enter the latitude of Anchorage, Alaska (about 54.667 degrees), we find that city has a rotational speed of approximately 600 mph.
- If we enter the latitude of Reykjavík, Iceland (64.0667 degrees), we find that capital has a rotational speed of approximately 453.8 mph.