14.3 Relationship of momentum to the center of mass by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
14.3 Relationship of momentum to the center of mass (optional)
We have already discussed the idea of the center of mass on p. 67, but using the concept of momentum we can now find a mathematical method for defining the center of mass, explain why the motion of an object's center of mass usually exhibits simpler motion than any other point, and gain a very simple and powerful way of understanding collisions.
The first step is to realize that the center of mass concept can be applied to systems containing more than one object. Even something like a wrench, which we think of as one object, is really made of many atoms. The center of mass is particularly easy to visualize in the case shown on the left, where two identical hockey pucks collide. It is clear on grounds of symmetry that their center of mass must be at the midpoint between them. After all, we previously defined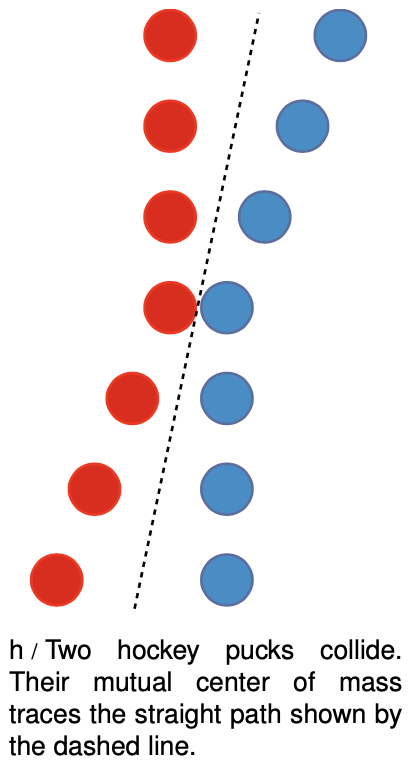 
the center of mass as the balance point, and if the two hockey pucks were joined with a very lightweight rod whose own mass was negligible, they would obviously balance at the midpoint. It doesn't matter that the hockey pucks are two separate objects. It is still true that the motion of their center of mass is exceptionally simple, just like that of the wrench's center of mass.
The `x` coordinate of the hockey pucks' center of mass is thus given by `x_"cm"=(x_1+x_2)"/"2`, i.e., the arithmetic average of their`x` coordinates. Why is its motion so simple? It has to do with conservation of momentum. Since the hockey pucks are not being acted on by any net external force, they constitute a closed system, and their total momentum is conserved. Their total momentum is
`mv_1+mv_2=m(v_1+v_2)`
`=m((Deltax_1)/(Deltat)+(Deltax_2)/(Deltat))`
`=m/(Deltat)Delta(x_1+x_2)`
`=m(2Deltax_cm)/(Deltat)`
`=m_"total"v_"cm"`
In other words, the total momentum of the system is the same as if all its mass was concentrated at the center of mass point. Since the total momentum is conserved, the `x` component of the center of mass's velocity vector cannot change. The same is also true for the other components, so the center of mass must move along a straight line at constant speed.
The above relationship between the total momentum and the motion of the center of mass applies to any system, even if it is not closed.
total momentum related to center of mass motion
The total momentum of any system is related to its total mass and the velocity of its center of mass by the equation
What about a system containing objects with unequal masses, or containing more than two objects? The reasoning above can be generalized to a weighted average
`x_"cm"=(m_1x_1+m_2x_2+...)/(m_1+m_2+...)`,
with similar equations for the `y` and `z` coordinates.
Momentum in different frames of reference
Absolute motion is supposed to be undetectable, i.e., the laws of physics are supposed to be equally valid in all inertial frames of reference. If we first calculate some momenta in one frame of reference and find that momentum is conserved, and then rework the whole problem in some other frame of reference that is moving with respect to the first, the numerical values of the momenta will all be different. Even so, momentum will still be conserved. All that matters is that we work a single problem in one consistent frame of reference.
One way of proving this is to apply the equation `p_"total"=m_"total"v_"cm"`. If the velocity of frame `B` relative to frame `A`is `v_"BA"`, then the only effect of changing frames of reference is to change `v_"cm"` from its original value to `v_"cm"+v_"BA"`. This adds a constant onto the momentum vector, which has no effect on conservation of momentum.
The center of mass frame of reference
A particularly useful frame of reference in many cases is the frame that moves along with the center of mass, called the center of mass (c.m.) frame. In this frame, the total momentum is zero. The following examples show how the center of mass frame can be a powerful tool for simplifying our understanding of collisions.
Example 12: A collision of pool balls viewed in the c.m. frame
If you move your head so that your eye is always above the point halfway in between the two pool balls, you are viewing things in the center of mass frame. In this frame, the balls come toward the center of mass at equal speeds. By symmetry, they must therefore recoil at equal speeds along the lines on which they entered. Since the balls have essentially swapped paths in the center of mass frame, the same must also be true in any other frame. This is the same result that required laborious algebra to prove previously without the concept of the center of mass frame.
Example 13: The slingshot effect
It is a counterintuitive fact that a spacecraft can pick up speed by swinging around a planet, if it arrives in the opposite direction compared to the planet's motion. Although there is no physical contact, we treat the encounter as a one-dimensional collision, and analyze it in the center of mass frame. Figure j shows such a “collision,” with a space probe whipping around Jupiter. In the sun's frame of reference, Jupiter is moving.
What about the center of mass frame? Since Jupiter is so much more massive than the spacecraft, the center of mass is essentially fixed at Jupiter's center, and Jupiter has zero velocity in the center of mass frame, as shown in figure k. The c.m. frame is moving to the left compared to the sun-fixed frame used in j, so the spacecraft's initial velocity is greater in this frame.
Things are simpler in the center of mass frame, because it is more symmetric. In the complicated sun-fixed frame, the incoming leg of the encounter is rapid, because the two bodies are rushing toward each other, while their separation on the outbound leg is more gradual, because Jupiter is trying to catch up. In the c.m. frame, Jupiter is sitting still, and there is perfect symmetry between the incoming and outgoing legs, so by symmetry we have `v_"1f"=-v_"1i"`. Going back to the sun-fixed frame, the spacecraft's final velocity is increased by the frames' motion relative to each other. In the sun-fixed frame, the spacecraft's velocity has increased greatly.
The result can also be understood in terms of work and energy. In Jupiter's frame, Jupiter is not doing any work on the spacecraft as it rounds the back of the planet, because the motion is perpendicular to the force. But in the sun's frame, the spacecraft's velocity vector at the same moment has a large component to the left, so Jupiter is doing work on it.
Discussion Questions
A Make up a numerical example of two unequal masses moving in one dimension at constant velocity, and verify the equation `p_"total"=m_"total"v_"cm"` over a time interval of one second.
B A more massive tennis racquet or baseball bat makes the ball fly off faster. Explain why this is true, using the center of mass frame. For simplicity, assume that the racquet or bat is simply sitting still before the collision, and that the hitter's hands do not make any force large enough to have a significant effect over the short duration of the impact.
14.3 Relationship of momentum to the center of mass by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.