17.3 Proofs by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
17.3 Proofs (optional)
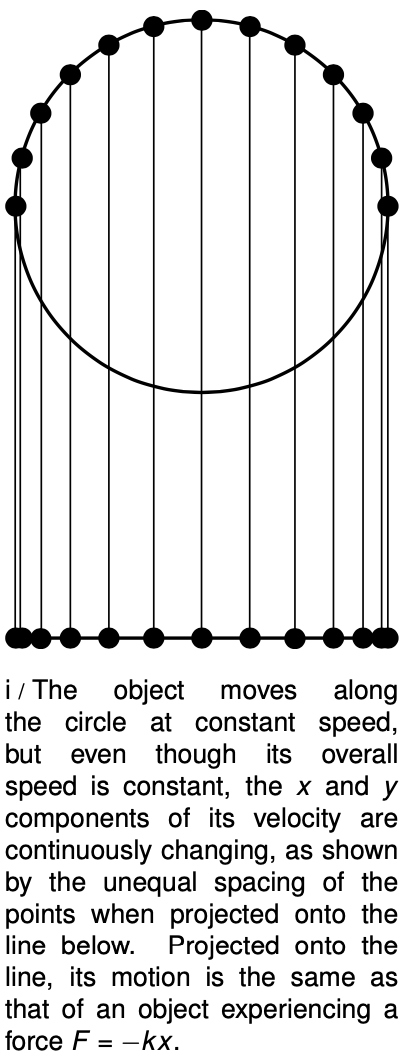In this section we prove (1) that a linear `F -x` graph gives sinusoidal motion, (2) that the period of the motion is `T=2pisqrt(m/k)`, and (3) that the period is independent of the amplitude. You may omit this section without losing the continuity of the chapter.
The basic idea of the proof can be understood by imagining that you are watching a child on a merry-go-round from far away. Because you are in the same horizontal plane as her motion, she appears to be moving from side to side along a line. Circular motion viewed edge-on doesn't just look like any kind of back-and-forth motion, it looks like motion with a sinusoidal `x-t` graph, because the sine and functions can be defined as the `x` and `y` coordinates of a point at angle `theta` on the unit circle. The idea of the proof, then, is to show that an object acted on by a force that varies as `F_X=-kX` has motion that is identical to circular motion projected down to one dimension. The `v^2`/`r` expression will also fall out at the end.
Example 5: The moons of Jupiter
Before moving on to the proof, we illustrate the concept using the moons of Jupiter. Their discovery by Galileo was an epochal event in astronomy, because it proved that not everything in the universe had to revolve around the earth as had been believed. Galileo's telescope was of poor quality by modern standards, but figure j shows a simulation of how Jupiter and its moons might appear at intervals of three hours through a large present-day instrument. Because we see the moons' circular orbits edge-on, they appear to perform sinusoidal vibrations. Over this time period, the innermost moon, Io, completes half a cycle.
For an object performing uniform circular motion, we have
The `x` component of the acceleration is therefore
`a_x=v^2/r costheta`,
where `theta` is the angle measured counterclockwise from the `x` axis. Applying Newton's second law,
`F_x/m=-v^2/rcostheta`, so
`F_x=-mv^2/rcostheta`.
Since our goal is an equation involving the period, it is natural to eliminate the variable `v="circumference/"T =2pir`/`T`, giving
`F_x=-(4pi^2mr)/T^ 2 costheta`.
`F_x=-(4pi^2m)/T^2 x`.
Since everything is constant in this equation except for `x`, we have proved that motion with force proportional to `x` is the same as circular motion projected onto a line, and therefore that a force proportional to `x` gives sinusoidal motion. Finally, we identify the constant factor of `4pi^2m`/`T^2` with `k`, and solving for `T` gives the desired equation for the period,
Since this equation is independent of `r`, `T` is independent of the amplitude, subject to the initial assumption of perfect `F=-kX` behavior, which in reality will only hold approximately for small `x`.
17.3 Proofs by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.