34.2 How much light is one photon by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
34.2 How much light is one photon?
The photoelectric effect
We have seen evidence that light energy comes in little chunks, so the next question to be asked is naturally how much energy is in one chunk. The most straightforward experimental avenue for addressing this question is a phenomenon known as the photoelectric effect. The photoelectric effect occurs when a photon strikes the surface of a solid object and knocks out an electron. It occurs continually all around you. It is happening right now at the surface of your skin and on the paper or computer screen from which you are reading these words. It does not ordinarily lead to any observable electrical effect, however, because on the average, free electrons are wandering back in just as frequently as they are being ejected. (If an object did somehow lose a significant number of electrons, its growing net positive charge would begin attracting the electrons back more and more strongly.)
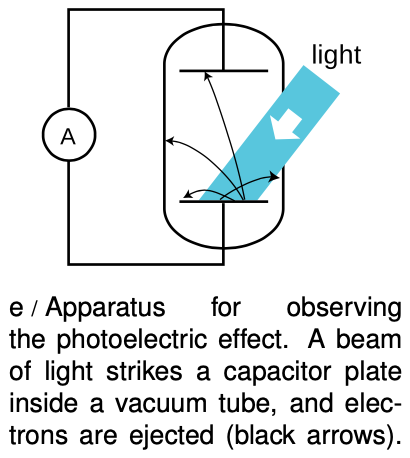Figure e shows a practical method for detecting the photoelectric effect. Two very clean parallel metal plates (the electrodes of a capacitor) are sealed inside a vacuum tube, and only one plate is exposed to light. Because there is a good vacuum between the plates, any ejected electron that happens to be headed in the right direction will almost certainly reach the other capacitor plate without colliding with any air molecules.
The illuminated (bottom) plate is left with a net positive charge, and the unilluminated (top) plate acquires a negative charge from the electrons deposited on it. There is thus an electric field between the plates, and it is because of this field that the electrons' paths are curved, as shown in the diagram. However, since vacuum is a good insulator, any electrons that reach the top plate are prevented from responding to the electrical attraction by jumping back across the gap. Instead they are forced to make their way around the circuit, passing through an ammeter. The ammeter measures the strength of the photoelectric effect.
An unexpected dependence on frequency
The photoelectric effect was discovered serendipitously by Heinrich Hertz in 1887, as he was experimenting with radio waves. He was not particularly interested in the phenomenon, but he did notice that the effect was produced strongly by ultraviolet light and more weakly by lower frequencies. Light whose frequency was lower than a certain critical value did not eject any electrons at all.1 This dependence on frequency didn't make any sense in terms of the classical wave theory of light. A light wave consists of electric and magnetic fields. The stronger the fields, i.e., the greater the wave's amplitude, the greater the forces that would be exerted on electrons that found themselves bathed in the light. It should have been amplitude (brightness) that was relevant, not frequency. The dependence on frequency not only proves that the wave model of light needs modifying, but with the proper interpretation it allows us to determine how much energy is in one photon, and it also leads to a connection between the wave and particle models that we need in order to reconcile them.
To make any progress, we need to consider the physical process by which a photon would eject an electron from the metal electrode. A metal contains electrons that are free to move around. Ordinarily, in the interior of the metal, such an electron feels attractive forces from atoms in every direction around it. The forces cancel out. But if the electron happens to find itself at the surface of the metal, the attraction from the interior side is not balanced out by any attraction from outside. In popping out through the surface the electron therefore loses some amount of energy `E_s`, which depends on the type of metal used.
Suppose a photon strikes an electron, annihilating itself and giving up all its energy to the electron.2 The electron will (1) lose kinetic energy through collisions with other electrons as it plows through the metal on its way to the surface; (2) lose an amount of kinetic energy equal to `E_s` as it emerges through the surface; and (3) lose more energy on its way across the gap between the plates, due to the electric field between the plates. Even if the electron happens to be right at the surface of the metal when it absorbs the photon, and even if the electric field between the plates has not yet built up very much, `E_s` is the bare minimum amount of energy that the electron must receive from the photon if it is to contribute to a measurable current. The reason for using very clean electrodes is to minimize `E_s` and make it have a definite value characteristic of the metal surface, not a mixture of values due to the various types of dirt and crud that are present in tiny amounts on all surfaces in everyday life.
We can now interpret the frequency dependence of the photoelectric effect in a simple way: apparently the amount of energy possessed by a photon is related to its frequency. A low-frequency red or infrared photon has an energy less than `E_s`, so a beam of them will not produce any current. A high-frequency blue or violet photon, on the other hand, packs enough of a punch to allow an electron to get out of the electrode. At frequencies higher than the minimum, the photoelectric current continues to increase with the frequency of the light because of effects (1) and (3).
Numerical relationship between energy and frequency
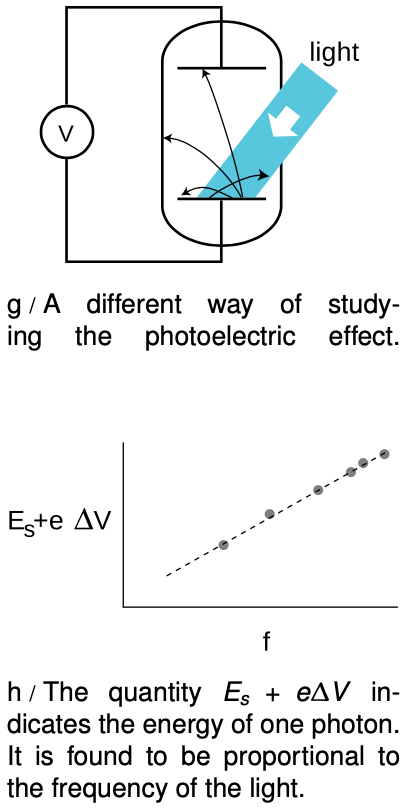Prompted by Einstein's photon paper, Robert Millikan (whom we encountered in ch. 26) figured out how to use the photoelectric effect to probe precisely the link between frequency and photon energy. Rather than going into the historical details of Millikan's actual experiments (a lengthy experimental program that occupied a large part of his professional career) we will describe a simple version, shown in figure g, that is used sometimes in college laboratory courses. The idea is simply to illuminate one plate of the vacuum tube with light of a single wavelength and monitor the voltage difference between the two plates as they charge up. Since the resistance of a voltmeter is very high (much higher than the resistance of an ammeter), we can assume to a good approximation that electrons reaching the top plate are stuck there permanently, so the voltage will keep on increasing for as long as electrons are making it across the vacuum tube.
At a moment when the voltage difference has a reached a value `DeltaV`, the minimum energy required by an electron to make it out of the bottom plate and across the gap to the other plate is `E_s+eDeltaV`. As `DeltaV` increases, we eventually reach a point at which `E_s+eDeltaV` equals the energy of one photon. No more electrons can cross the gap, and the reading on the voltmeter stops rising. The quantity `E_s+eDeltaV` now tells us the energy of one photon. If we determine this energy for a variety of frequencies, h, we find the following simple relationship between the energy of a photon and the frequency of the light:
where `h` is a constant with a numerical value of `6.63×10^(-34) J*s`.
Note how the equation brings the wave and particle models of light under the same roof: the left side is the energy of one particle of light, while the right side is the frequency of the same light, interpreted as a wave. The constant `h` is known as Planck's constant (see historical note on page 947).
self-check:
How would you extract `h` from the graph in figure h? What if you didn't even know `E_s` in advance, and could only graph `eDeltaV` versus `f`?
(answer in the back of the PDF version of the book)
Since the energy of a photon is `hf`, a beam of light can only have energies of `hf`, `2hf`, `3hf`, etc. Its energy is quantized `-` there is no such thing as a fraction of a photon. Quantum physics gets its name from the fact that it quantizes things like energy, momentum, and angular momentum that had previously been thought to be smooth, continuous and infinitely divisible.
Example 1: Number of photons emitted by a lightbulb per second
`=>` Roughly how many photons are emitted by a 100-W lightbulb in 1 second?
`=>` People tend to remember wavelengths rather than frequencies for visible light. The bulb emits photons with a range of frequencies and wavelengths, but let's take 600 nm as a typical wavelength for purposes of estimation. The energy of a single photon is
`E_"photon"``=hf`
A power of 100 W means 100 joules per second, so the number of photons is
`(100J)/E_"photon"=(100J)/(hc"/"lambda)approx3×10^20`.
This hugeness of this number is consistent with the correspondence principle. The experiments that established the classical theory of optics weren't wrong. They were right, within their domain of applicability, in which the number of photons was so large as to be indistinguishable from a continuous beam.
Example 2: Measuring the wave
When surfers are out on the water waiting for their chance to catch a wave, they're interested in both the height of the waves and when the waves are going to arrive. In other words, they observe both the amplitude and phase of the waves, and it doesn't matter to them that the water is granular at the molecular level. The correspondence principle requires that we be able to do the same thing for electromagnetic waves, since the classical theory of electricity and magnetism was all stated and verified experimentally in terms of the fields `E` and `B`, which are the amplitude of an electromagnetic wave. The phase is also necessary, since the laws of induction predict different results depending on whether an oscillating field is on its way up or on its way back down.
This is a more demanding application of the correspondence principle than the one in example 1, since amplitudes and phases constitute more detailed information than the over-all intensity of a beam of light. Eyeball measurements can't detect this type of information, since the eye is much bigger than a wavelength, but for example an AM radio receiver can do it with radio waves, since the wavelength for a station at 1000 kHz is about 300 meters, which is much larger than the antenna. The correspondence principle demands that we be able to explain this in terms of the photon theory, and this requires not just that we have a large number of photons emitted by the transmitter per second, as in example 1, but that even by the time they spread out and reach the receiving antenna, there should be many photons overlapping each other within a space of one cubic wavelength. Problem 13 on p. 958 verifies that the number is in fact extremely large.
Example 3: Momentum of a photon
`=>` According to the theory of relativity, the momentum of a beam of light is given by `p=E/c`
(see homework problem 12 on page 789). Apply this to find the momentum of a single photon in terms of its frequency, and in terms of its wavelength.
`=>` Combining the equations `p=E/c` and `E=hf`, we find
To reexpress this in terms of wavelength, we use :
`p=(hf)/(flambda)`
The second form turns out to be simpler.
Discussion Questions
A The photoelectric effect only ever ejects a very tiny percentage of the electrons available near the surface of an object. How well does this agree with the wave model of light, and how well with the particle model? Consider the two different distance scales involved: the wavelength of the light, and the size of an atom, which is on the order of `10^(-10)` or `10^(-9) m`.
B What is the significance of the fact that Planck's constant is numerically very small? How would our everyday experience of light be different if it was not so small?
C How would the experiments described above be affected if a single electron was likely to get hit by more than one photon?
D Draw some representative trajectories of electrons for `DeltaV=0`, `DeltaV` less than the maximum value, and `DeltaV` greater than the maximum value.
E Does `E=hf` imply that a photon changes its energy when it passes from one transparent material into another substance with a different index of refraction?
34.2 How much light is one photon by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.