24.7 Doppler shifts and clock time by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
24.7 Doppler shifts and clock time (optional)
Figure u shows our now-familiar method of visualizing a Lorentz transformation, in a case where the numbers come out to be particularly simple. This diagram has two geometrical features that we have referred to before without digging into their physical significance: the stretch factor of the diagonals, and the area. In this section we'll see that the former can be related to the Doppler effect, and the latter to clock time.
Doppler shifts of light
When Doppler shifts happen to ripples on a pond or the sound waves from an airplane, they can depend on the relative motion of three different objects: the source, the receiver, and the medium. But light waves don't have a medium. Therefore Doppler shifts of light can only depend on the relative motion of the source and observer.
One simple case is the one in which the relative motion of the source and the receiver is perpendicular to the line connecting them. That is, the motion is transverse. Nonrelativistic Doppler shifts happen because the distance between the source and receiver is changing, so in nonrelativistic physics we don't expect any Doppler shift at all when the motion is transverse, and this is what is in fact observed to high precision. For example, the photo shows shortened and lengthened wavelengths to the right and left, along the source's line of motion, but an observer above or below the source measures just the normal, unshifted wavelength and frequency. But relativistically, we have a time dilation effect, so for light waves emitted transversely, there is a Doppler shift of `1"/"gamma` in frequency (or `gamma` in wavelength).
The other simple case is the one in which the relative motion of the source and receiver is longitudinal, i.e., they are either approaching or receding from one another. For example, distant galaxies are receding from our galaxy due to the expansion of the universe, and this expansion was originally detected because Doppler shifts toward the red (low-frequency) end of the spectrum were observed.
Nonrelativistically, we would expect the light from such a galaxy to be Doppler shifted down in frequency by some factor, which would depend on the relative velocities of three different objects: the source, the wave's medium, and the receiver. Relativistically, things get simpler, because light isn't a vibration of a physical medium, so the Doppler shift can only depend on a single velocity `v`, which is the rate at which the separation between the source and the receiver is increasing.
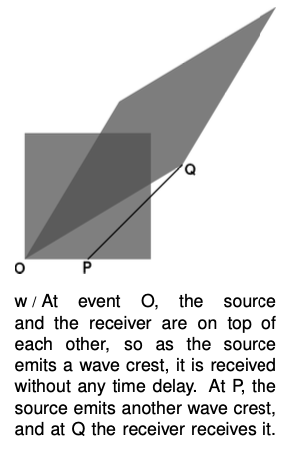The square in figure w is the “graph paper” used by someone who considers the source to be at rest, while the parallelogram plays a similar role for the receiver. The figure is drawn for the case where `v=3"/"5` (in units where `c=1`), and in this case the stretch factor of the long diagonal is 2. To keep the area the same, the short diagonal has to be squished to half its original size. But now it's a matter of simple geometry to show that OP equals half the width of the square, and this tells us that the Doppler shift is a factor of 1/2 in frequency. That is, the squish factor of the short diagonal is interpreted as the Doppler shift. To get this as a general equation for velocities other than 3/5, one can show by straightforward fiddling with the result of part c of problem 2 on p. 673 that the Doppler shift is
Here `v>0` is the case where the source and receiver are getting farther apart, `v<0` the case where they are approaching. (This is the opposite of the sign convention used in section 19.5. It is convenient to change conventions here so that we can use positive values of `v` in the case of cosmological red-shifts, which are the most important application.)
Suppose that Alice stays at home on earth while her twin Betty takes off in her rocket ship at 3/5 of the speed of light. When I first learned relativity, the thing that caused me the most pain was understanding how each observer could say that the other was the one whose time was slow. It seemed to me that if I could take a pill that would speed up my mind and my body, then naturally I would see everybody else as being slow. Shouldn't the same apply to relativity? But suppose Alice and Betty get on the radio and try to settle who is the fast one and who is the slow one. Each twin's voice sounds slooooowed doooowwwwn to the other. If Alice claps her hands twice, at a time interval of one second by her clock, Betty hears the hand-claps coming over the radio two seconds apart, but the situation is exactly symmetric, and Alice hears the same thing if Betty claps. Each twin analyzes the situation using a diagram identical to w, and attributes her sister's observations to a complicated combination of time distortion, the time taken by the radio signals to propagate, and the motion of her twin relative to her.
self-check:
Turn your book upside-down and reinterpret figure w.
(answer in the back of the PDF version of the book)
Example 11: A symmetry property of the Doppler effect
Suppose that A and B are at rest relative to one another, but C is moving along the line between A and B. A transmits a signal to C, who then retransmits it to B. The signal accumulates two Doppler shifts, and the result is their product `D(v)D(-v)`. But this product must equal 1, so we must have `D(-v)D(v)=1`, which can be verified directly from the equation.
Example 12: The Ives-Stilwell experiment
The result of example 11 was the basis of one of the earliest laboratory tests of special relativity, by Ives and Stilwell in 1938. They observed the light emitted by excited by a beam of `H_2^+` and `H_3^+` ions with speeds of a few tenths of a percent of `c`. Measuring the light from both ahead of and behind the beams, they found that the product of the Doppler shifts `D(v)D(-v)` was equal to 1, as predicted by relativity. If relativity had been false, then one would have expected the product to differ from 1 by an amount that would have been detectable in their experiment. In 2003, Saathoff et al. carried out an extremely precise version of the Ives-Stilwell technique with `Li^+` ions moving at 6.4% of `c`. The frequencies observed, in units of MHz, were:
The results show incredibly precise agreement between `f_o` and `sqrt(f_oD(-v)*f_oD(v))`, as expected relativistically because `D(v)D(-v)` is supposed to equal 1. The agreement extends to 9 significant figures, whereas if relativity had been false there should have been a relative disagreement of about `v^2=.004`, i.e., a discrepancy in the third significant figure. The spectacular agreement with theory has made this experiment a lightning rod for anti-relativity kooks.
We saw on p. 682 that relativistic velocities should not be expected to be exactly additive, and problem 1 on p. 700 verifies this in the special case where A moves relative to B at `0.6c` and B relative to C at `0.6c` `-` the result not being `1.2c`. The relativistic Doppler shift provides a simple way of deriving a general equation for the relativistic combination of velocities; problem 21 on p. 705 guides you through the steps of this derivation.
Clock time
On p. 658 we proved that the Lorentz transformation doesn't change the area of a shape in the `x-t` plane. We used this only as a stepping stone toward the Lorentz transformation, but it is natural to wonder whether this kind of area has any physical interest of its own.
The equal-area result is not relativistic, since the proof never appeals to property 5 on page 654. Cases I and II on page 657 also have the equal-area property. We can see this clearly in a Galilean transformation like figure g on p. 655, where the distortion of the rectangle could be accomplished by cutting it into vertical slices and then displacing the slices upward without changing their areas.
But the area does have a nice interpretation in the relativistic case. Suppose that we have events A (Charles VII is restored to the throne) and B (Joan of Arc is executed). Now imagine that technologically advanced aliens want to be present at both A and B, but in the interim they wish to fly away in their spaceship, be present at some other event P (perhaps a news conference at which they give an update on the events taking place on earth), but get back in time for B. Since nothing can go faster than `c` (which we take to equal 1 in appropriate units), P cannot be too far away. The set of all possible events P forms a rectangle, figure x/1, in the `x-t` plane that has A and B at opposite corners and whose edges have slopes equal to `±1`. We call this type of rectangle a light-rectangle, because its sides could represent the motion of rays of light.
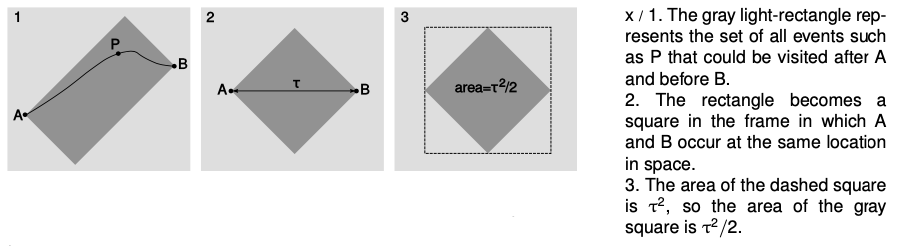
The area of this rectangle will be the same regardless of one's frame of reference. In particular, we could choose a special frame of reference, panel 2 of the figure, such that A and B occur in the same place. (They do not occur at the same place, for example, in the sun's frame, because the earth is spinning and going around the sun.) Since the speed `c`, which equals 1 in our units, is the same in all frames of reference, and the sides of the rectangle had slopes `±1` in frame 1, they must still have slopes `+-1` in frame 2. The rectangle becomes a square with its diagonals parallel to the `x` and `t` axes, and the length of these diagonals equals the time `tau` elapsed on a clock that is at rest in frame 2, i.e., a clock that glides through space at constant velocity from A to B, meeting up with the planet earth at the appointed time. As shown in panel 3 of the figure, the area of the gray regions can be interpreted as half the square of this gliding-clock time. If events A and B are separated by a distance `x` and a time `t`, then in general `t^2-x^2` gives the square of the gliding-clock time.
When `|x|` is greater than `|t|`, events A and B are so far apart in space and so close together in time that it would be impossible to have a cause and effect relationship between them, since `c=1` is the maximum speed of cause and effect. In this situation `t^2-x^2` is negative and cannot be interpreted as a clock time, but it can be interpreted as minus the square of the distance between A and B as measured by rulers at rest in a frame in which A and B are simultaneous.
No matter what, `t^2-x^2` is the same as measured in all frames of reference. Geometrically, it plays the same role in the `x-t` plane that ruler measurements play in the Euclidean plane. In Euclidean geometry, the ruler-distance between any two points stays the same regardless of rotation, i.e., regardless of the angle from which we view the scene; according to the Pythagorean theorem, the square of this distance is `x^2+y^2`. In the `x-t` plane, `t^2-x^2` stays the same regardless of the frame of reference.
To avoid overloading the reader with terms to memorize, some commonly used terminology is relegated to problem 22 on p. 706.
24.7 Doppler shifts and clock time by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.