35.2 Dispersive waves by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
35.2 Dispersive waves (optional calculus-based section)
A colleague of mine who teaches chemistry loves to tell the story about an exceptionally bright student who, when told of the equation `p=h/lambda`, protested, “But when I derived it, it had a factor of `2`!” The issue that's involved is a real one, albeit one that could be glossed over (and is, in most textbooks) without raising any alarms in the mind of the average student. The present optional section addresses this point; it is intended for the student who wishes to delve a little deeper.
Here's how the now-legendary student was presumably reasoning. We start with the equation , which is valid for any sine wave, whether it's quantum or classical. Let's assume we already know `E=hf`, and are trying to derive the relationship between wavelength and momentum:
`=(vh)/E`
`=(vh)/(1/2mv^2)`
`=(2h)/(mv)`
`=(2h)/p`
The reasoning seems valid, but the result does contradict the accepted one, which is after all solidly based on experiment.
The mistaken assumption is that we can figure everything out in terms of pure sine waves. Mathematically, the only wave that has a perfectly well defined wavelength and frequency is a sine wave, and not just any sine wave but an infinitely long one, c. The unphysical thing about such a wave is that it has no leading or trailing edge, so it can never be said to enter or leave any particular region of space. Our derivation made use of the velocity, `v`, and if velocity is to be a meaningful concept, it must tell us how quickly stuff (mass, energy, momentum,...) is transported from one region of space to another. Since an infinitely long sine wave doesn't remove any stuff from one region and take it to another, the “velocity of its stuff” is not a well defined concept.
Of course the individual wave peaks do travel through space, and one might think that it would make sense to associate their speed with the “speed of stuff,” but as we will see, the two velocities are in general unequal when a wave's velocity depends on wavelength. Such a wave is called a dispersive wave, because a wave pulse consisting of a superposition of waves of different wavelengths will separate (disperse) into its separate wavelengths as the waves move through space at different speeds. Nearly all the waves we have encountered have been nondispersive. For instance, sound waves and light waves (in a vacuum) have speeds independent of wavelength. A water wave is one good example of a dispersive wave. Long-wavelength water waves travel faster, so a ship at sea that encounters a storm typically sees the long-wavelength parts of the wave first. When dealing with dispersive waves, we need symbols and words to distinguish the two speeds. The speed at which wave peaks move is called the phase velocity, `v_p`, and the speed at which “stuff” moves is called the group velocity, `v_g`.
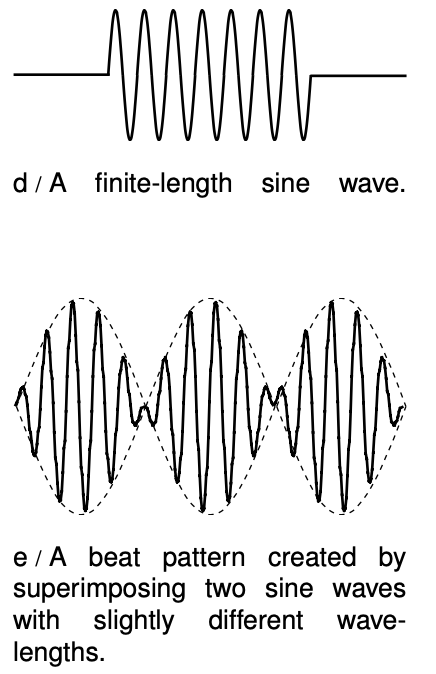An infinite sine wave can only tell us about the phase velocity, not the group velocity, which is really what we would be talking about when we referred to the speed of an electron. If an infinite sine wave is the simplest possible wave, what's the next best thing? We might think the runner up in simplicity would be a wave train consisting of a chopped-off segment of a sine wave, d. However, this kind of wave has kinks in it at the end. A simple wave should be one that we can build by superposing a small number of infinite sine waves, but a kink can never be produced by superposing any number of infinitely long sine waves.
Actually the simplest wave that transports stuff from place to place is the pattern shown in figure e. Called a beat pattern, it is formed by superposing two sine waves whose wavelengths are similar but not quite the same. If you have ever heard the pulsating howling sound of musicians in the process of tuning their instruments to each other, you have heard a beat pattern. The beat pattern gets stronger and weaker as the two sine waves go in and out of phase with each other. The beat pattern has more “stuff” (energy, for example) in the areas where constructive interference occurs, and less in the regions of cancellation. As the whole pattern moves through space, stuff is transported from some regions and into other ones.
If the frequency of the two sine waves differs by `10%`, for instance, then ten periods will be occur between times when they are in phase. Another way of saying it is that the sinusoidal “envelope” (the dashed lines in figure e) has a frequency equal to the difference in frequency between the two waves. For instance, if the waves had frequencies of `100` Hz and `110` Hz, the frequency of the envelope would be `10`Hz.
To apply similar reasoning to the wavelength, we must define a quantity `z=1"/"lambda` that relates to wavelength in the same way that frequency relates to period. In terms of this new variable, the `z` of the envelope equals the difference between the `z`'s of the two sine waves.
The group velocity is the speed at which the envelope moves through space. Let `Deltaf` and `Deltaz` be the differences between the frequencies and `z`'s of the two sine waves, which means that they equal the frequency and `z` of the envelope. The group velocity is `v_g=f_"envelope"lambda_"envelope"=(Deltaf)"/"(Deltaz)`. If `Deltaf` and `Deltaz` are sufficiently small, we can approximate this expression as a derivative,
`v_g=(df)/(dz)`.
This expression is usually taken as the definition of the group velocity for wave patterns that consist of a superposition of sine waves having a narrow range of frequencies and wavelengths. In quantum mechanics, with `f=E"/"h` and `z=p"/"h`, we have `v_g=(dE)"/"(dp)`. In the case of a nonrelativistic electron the relationship between energy and momentum is `E=p^2"/"(2m)`, so the group velocity is `(dE)"/"(dp)=p"/"m=v`, exactly what it should be. It is only the phase velocity that differs by a factor of two from what we would have expected, but the phase velocity is not the physically important thing.
35.2 Dispersive waves by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.