15.1 Conservation of angular momentum by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
15.1 Conservation of angular momentum
When most people think of rotation, they think of a solid object like a wheel rotating in a circle around a fixed point. Examples of this type of rotation, called rigid rotation or rigid-body rotation, include a spinning top, a seated child's swinging leg, and a helicopter's spinning propeller. Rotation, however, is a much more general phenomenon, and includes noncircular examples such as a comet in an elliptical orbit around the sun, or a cyclone, in which the core completes a circle more quickly than the outer parts.
If there is a numerical measure of rotational motion that is a conserved quantity, then it must include nonrigid cases like these, since nonrigid rotation can be traded back and forth with rigid rotation. For instance, there is a trick for finding out if an egg is raw or hardboiled. If you spin a hardboiled egg and then stop it briefly with your finger, it stops dead. But if you do the same with a raw egg, it springs back into rotation because the soft interior was still swirling around within the momentarily motionless shell. The pattern of flow of the liquid part is presumably very complex and nonuniform due to the asymmetric shape of the egg and the different consistencies of the yolk and the white, but there is apparently some way to describe the liquid's total amount of rotation with a single number, of which some percentage is given back to the shell when you release it.
The best strategy is to devise a way of defining the amount of rotation of a single small part of a system. The amount of rotation of a system such as a cyclone will then be defined as the total of all the contributions from its many small parts.
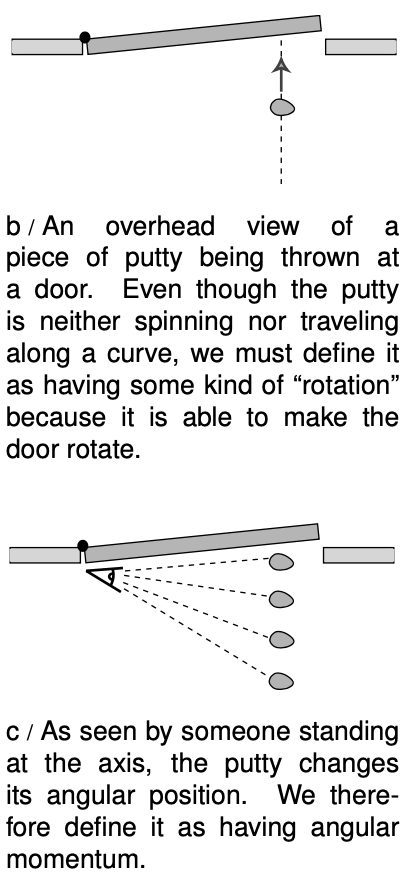
The quest for a conserved quantity of rotation even requires us to broaden the rotation concept to include cases where the motion doesn't repeat or even curve around. If you throw a piece of putty at a door, the door will recoil and start rotating. The putty was traveling straight, not in a circle, but if there is to be a general conservation law that can cover this situation, it appears that we must describe the putty as having had some “rotation,” which it then gave up to the door. The best way of thinking about it is to attribute rotation to any moving object or part of an object that changes its angle in relation to the axis of rotation. In the putty-and-door example, the hinge of the door is the natural point to think of as an axis, and the putty changes its angle as seen by someone standing at the hinge. For this reason, the conserved quantity we are investigating is called angular momentum. The symbol for angular momentum can't be `a` or `m`, since those are used for acceleration and mass, so the symbol `L` is arbitrarily chosen instead.
Imagine a 1-kg blob of putty, thrown at the door at a speed of 1 m/s, which hits the door at a distance of 1 m from the hinge. We define this blob to have 1 unit of angular momentum. When it hits the door, the door will recoil and start rotating. We can use the speed at which the door recoils as a measure of the angular momentum the blob brought in.
Experiments show, not surprisingly, that a 2-kg blob thrown in the same way makes the door rotate twice as fast, so the angular momentum of the putty blob must be proportional to mass,
`Lpropm`.
Similarly, experiments show that doubling the velocity of the blob will have a doubling effect on the result, so its angular momentum must be proportional to its velocity as well,
`Lpropmv`.
You have undoubtedly had the experience of approaching a closed door with one of those bar-shaped handles on it and pushing on the wrong side, the side close to the hinges. You feel like an idiot, because you have so little leverage that you can hardly budge the door. The same would be true with the putty blob. Experiments would show that the amount of rotation the blob can give to the door is proportional to the distance, `r`,
`Lpropmvr`.
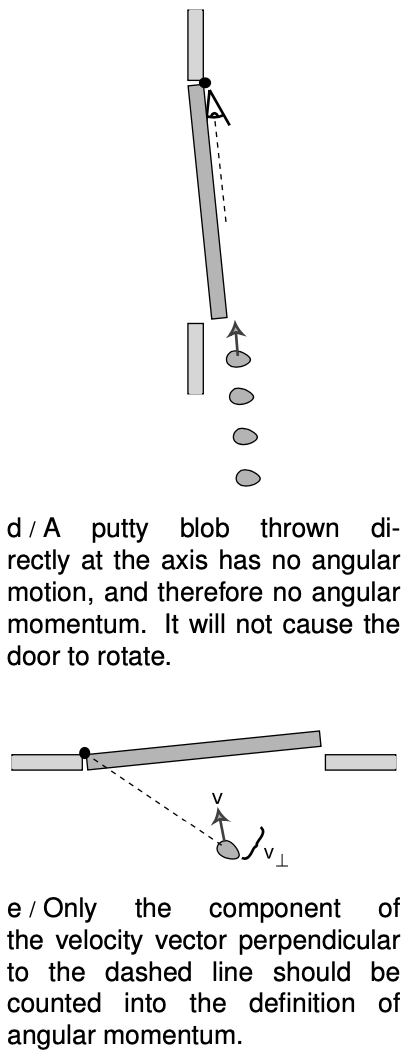
We are almost done, but there is one missing ingredient. We know on grounds of symmetry that a putty ball thrown directly inward toward the hinge will have no angular momentum to give to the door. After all, there would not even be any way to decide whether the ball's rotation was clockwise or counterclockwise in this situation. It is therefore only the component of the blob's velocity vector perpendicular to the door that should be counted in its angular momentum,
More generally, `v_(bot)` should be thought of as the component of the object's velocity vector that is perpendicular to the line joining the object to the axis of rotation.
We find that this equation agrees with the definition of the original putty blob as having one unit of angular momentum, and we can now see that the units of angular momentum are `kg*m^2"/"s`. This gives us a way of calculating the angular momentum of any material object or any system consisting of material objects:
Note that `r` is not necessarily the radius of a circle. (As implied by the qualifiers, matter isn't the only thing that can have angular momentum. Light can also have angular momentum, and the above equation would not apply to light.)
Conservation of angular momentum has been verified over and over again by experiment, and is now believed to be one of the three most fundamental principles of physics, along with conservation of energy and momentum.
Example 1: A figure skater pulls her arms in
When a figure skater is twirling, there is very little friction between her and the ice, so she is essentially a closed system, and her angular momentum is conserved. If she pulls her arms in, she is decreasing `r` for all the atoms in her arms. It would violate conservation of angular momentum if she then continued rotating at the same speed, i.e., taking the same amount of time for each revolution, because her arms' contributions to her angular momentum would have decreased, and no other part of her would have increased its angular momentum. This is impossible because it would violate conservation of angular momentum. If her total angular momentum is to remain constant, the decrease in `r` for her arms must be compensated for by an overall increase in her rate of rotation. That is, by pulling her arms in, she substantially reduces the time for each rotation.
Example 2: Changing the axis
An object's angular momentum can be different depending on the axis about which it rotates. Figure g shows two double-exposure photographs a viola player tipping the bow in order to cross from one string to another. Much more angular momentum is required when playing near the bow's handle, called the frog, as in the panel on the right; not only are most of the atoms in the bow at greater distances, `r`, from the axis of rotation, but the ones in the tip also have more momentum, `p`. It is difficult for the player to quickly transfer a large angular momentum into the bow, and then transfer it back out just as quickly. (In the language of section 15.4, large torques are required.) This is one of the reasons that string players tend to stay near the middle of the bow as much as possible.
Example 3: Earth's slowing rotation and the receding moon
As noted in chapter 1, the earth's rotation is actually slowing down very gradually, with the kinetic energy being dissipated as heat by friction between the land and the tidal bulges raised in the seas by the earth's gravity. Does this mean that angular momentum is not really perfectly conserved? No, it just means that the earth is not quite a closed system by itself. If we consider the earth and moon as a system, then the angular momentum lost by the earth must be gained by the moon somehow. In fact very precise measurements of the distance between the earth and the moon have been carried out by bouncing laser beams off of a mirror left there by astronauts, and these measurements show that the moon is receding from the earth at a rate of 4 centimeters per year! The moon's greater value of `r` means that it has a greater angular momentum, and the increase turns out to be exactly the amount lost by the earth. In the days of the dinosaurs, the days were significantly shorter, and the moon was closer and appeared bigger in the sky.
But what force is causing the moon to speed up, drawing it out into a larger orbit? It is the gravitational forces of the earth's tidal bulges. The effect is described qualitatively in the caption of the figure. The result would obviously be extremely difficult to calculate directly, and this is one of those situations where a conservation law allows us to make precise quantitative statements about the outcome of a process when the calculation of the process itself would be prohibitively complex.
Restriction to rotation in a plane
Is angular momentum a vector, or a scalar? It does have a direction in space, but it's a direction of rotation, not a straight-line direction like the directions of vectors such as velocity or force. It turns out (see problem 29) that there is a way of defining angular momentum as a vector, but in this book the examples will be confined to a single plane of rotation, i.e., effectively two-dimensional situations. In this special case, we can choose to visualize the plane of rotation from one side or the other, and to define clockwise and counterclockwise rotation as having opposite signs of angular momentum.
Discussion Question
A Conservation of plain old momentum, `p`, can be thought of as the greatly expanded and modified descendant of Galileo's original principle of inertia, that no force is required to keep an object in motion. The principle of inertia is counterintuitive, and there are many situations in which it appears superficially that a force is needed to maintain motion, as maintained by Aristotle. Think of a situation in which conservation of angular momentum, `L`, also seems to be violated, making it seem incorrectly that something external must act on a closed system to keep its angular momentum from “running down.”
15.1 Conservation of angular momentum by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.