14.2 Collisions in one dimension by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
14.2 Collisions in one dimension
Physicists employ the term “collision” in a broader sense than ordinary usage, applying it to any situation where objects interact for a certain period of time. A bat hitting a baseball, a radioactively emitted particle damaging DNA, and a gun and a bullet going their separate ways are all examples of collisions in this sense. Physical contact is not even required. A comet swinging past the sun on a hyperbolic orbit is considered to undergo a collision, even though it never touches the sun. All that matters is that the comet and the sun exerted gravitational forces on each other.
The reason for broadening the term “collision” in this way is that all of these situations can be attacked mathematically using the same conservation laws in similar ways. In the first example, conservation of momentum is all that is required.
Example 10: Getting rear-ended
`=>` Ms. Chang is rear-ended at a stop light by Mr. Nelson, and sues to make him pay her medical bills. He testifies that he was only going 35 miles per hour when he hit Ms. Chang. She thinks he was going much faster than that. The cars skidded together after the impact, and measurements of the length of the skid marks and the coefficient of friction show that their joint velocity immediately after the impact was 19 miles per hour. Mr. Nelson's Nissan weighs 3100 pounds, and Ms. Chang 's Cadillac weighs 5200 pounds. Is Mr. Nelson telling the truth?
`=>` Since the cars skidded together, we can write down the equation for conservation of momentum using only two velocities, `v` for Mr. Nelson's velocity before the crash, and `v'` for their joint velocity afterward:
`m_Nv=m_Nv'+m_Cv'`.
Solving for the unknown, `v`, we find
`v=(1+m_C/m_N)v'`.
Although we are given the weights in pounds, a unit of force, the ratio of the masses is the same as the ratio of the weights, and we find `v=51` miles per hour. He is lying.
The above example was simple because both cars had the same velocity afterward. In many one-dimensional collisions, however, the two objects do not stick. If we wish to predict the result of such a collision, conservation of momentum does not suffice, because both velocities after the collision are unknown, so we have one equation in two unknowns.
Conservation of energy can provide a second equation, but its application is not as straightforward, because kinetic energy is only the particular form of energy that has to do with motion. In many collisions, part of the kinetic energy that was present before the collision is used to create heat or sound, or to break the objects or permanently bend them. Cars, in fact, are carefully designed to crumple in a collision. Crumpling the car uses up energy, and that's good because the goal is to get rid of all that kinetic energy in a relatively safe and controlled way. At the opposite extreme, a superball is “super” because it emerges from a collision with almost all its original kinetic energy, having only stored it briefly as potential energy while it was being squashed by the impact.
Collisions of the superball type, in which almost no kinetic energy is converted to other forms of energy, can thus be analyzed more thoroughly, because they have `KE_f=KE_i`, as opposed to the less useful inequality `KE_fltKE_i` for a case like a tennis ball bouncing on grass.
Example 11: Pool balls colliding head-on
`=>` Two pool balls collide head-on, so that the collision is restricted to one dimension. Pool balls are constructed so as to lose as little kinetic energy as possible in a collision, so under the assumption that no kinetic energy is converted to any other form of energy, what can we predict about the results of such a collision?
`=>` Pool balls have identical masses, so we use the same symbol `m` for both. Conservation of momentum and no loss of kinetic energy give us the two equations
`mv_"1i"+mv_"2i"=mv_"1f"+mv_"2f"`
`1/2 mv_"1i"^2+mv_"2i"^2=mv_"1f"^2+mv_"2f"^2`
The masses and the factors of 1/2 can be divided out, and we eliminate the cumbersome subscripts by replacing the symbols `v_"1i",...` with the symbols `A,B,C`, and` D`:
`A+B=C+D`
`A^2+B^2=C^2+D^2`.
A little experimentation with numbers shows that given values of `A` and `B` , it is impossible to find `C` and `D` that satisfy these equations unless `C` and `D` equal `A` and `B`, or `C` and `D` are the same as `A` and `B` but swapped around. A formal proof of this fact is given in the sidebar. In the special case where ball 2 is initially at rest, this tells us that ball 1 is stopped dead by the collision, and ball 2 heads off at the velocity originally possessed by ball 1. This behavior will be familiar to players of pool.
Often, as in the example above, the details of the algebra are the least interesting part of the problem, and considerable physical insight can be gained simply by counting the number of unknowns and comparing to the number of equations. Suppose a beginner at pool notices a case where her cue ball hits an initially stationary ball and stops dead. “Wow, what a good trick,” she thinks. “I bet I could never do that again in a million years.” But she tries again, and finds that she can't help doing it even if she doesn't want to. Luckily she has just learned about collisions in her physics course. Once she has written down the equations for conservation of energy and no loss of kinetic energy, she really doesn't have to complete the algebra. She knows that she has two equations in two unknowns, so there must be a well-defined solution. Once she has seen the result of one such collision, she knows that the same thing must happen every time. The same thing would happen with colliding marbles or croquet balls. It doesn't matter if the masses or velocities are different, because that just multiplies both equations by some constant factor.
The discovery of the neutron
This was the type of reasoning employed by James Chadwick in his 1932 discovery of the neutron. At the time, the atom was imagined to be made out of two types of fundamental particles, protons and electrons. The protons were far more massive, and clustered together in the atom's core, or nucleus. Attractive electrical forces caused the electrons to orbit the nucleus in circles, in much the same way that gravitational forces kept the planets from cruising out of the solar system. Experiments showed that the helium nucleus, for instance, exerted exactly twice as much electrical force on an electron as a nucleus of hydrogen, the smallest atom, and this was explained by saying that helium had two protons to hydrogen's one. The trouble was that according to this model, helium would have two electrons and two protons, giving it precisely twice the mass of a hydrogen atom with one of each. In fact, helium has about four times the mass of hydrogen.
Chadwick suspected that the helium nucleus possessed two additional particles of a new type, which did not participate in electrical forces at all, i.e., were electrically neutral. If these particles had very nearly the same mass as protons, then the four-to-one mass ratio of helium and hydrogen could be explained. In 1930, a new type of radiation was discovered that seemed to fit this description. It was electrically neutral, and seemed to be coming from the nuclei of light elements that had been exposed to other types of radiation. At this time, however, reports of new types of particles were a dime a dozen, and most of them turned out to be either clusters made of previously known particles or else previously known particles with higher energies. Many physicists believed that the “new” particle that had attracted Chadwick's interest was really a previously known particle called a gamma ray, which was electrically neutral. Since gamma rays have no mass, Chadwick decided to try to determine the new particle's mass and see if it was nonzero and approximately equal to the mass of a proton.
Unfortunately a subatomic particle is not something you can just put on a scale and weigh. Chadwick came up with an ingenious solution. The masses of the nuclei of the various chemical elements were already known, and techniques had already been developed for measuring the speed of a rapidly moving nucleus. He therefore set out to bombard samples of selected elements with the mysterious new particles. When a direct, head-on collision occurred between a mystery particle and the nucleus of one of the target atoms, the nucleus would be knocked out of the atom, and he would measure its velocity.
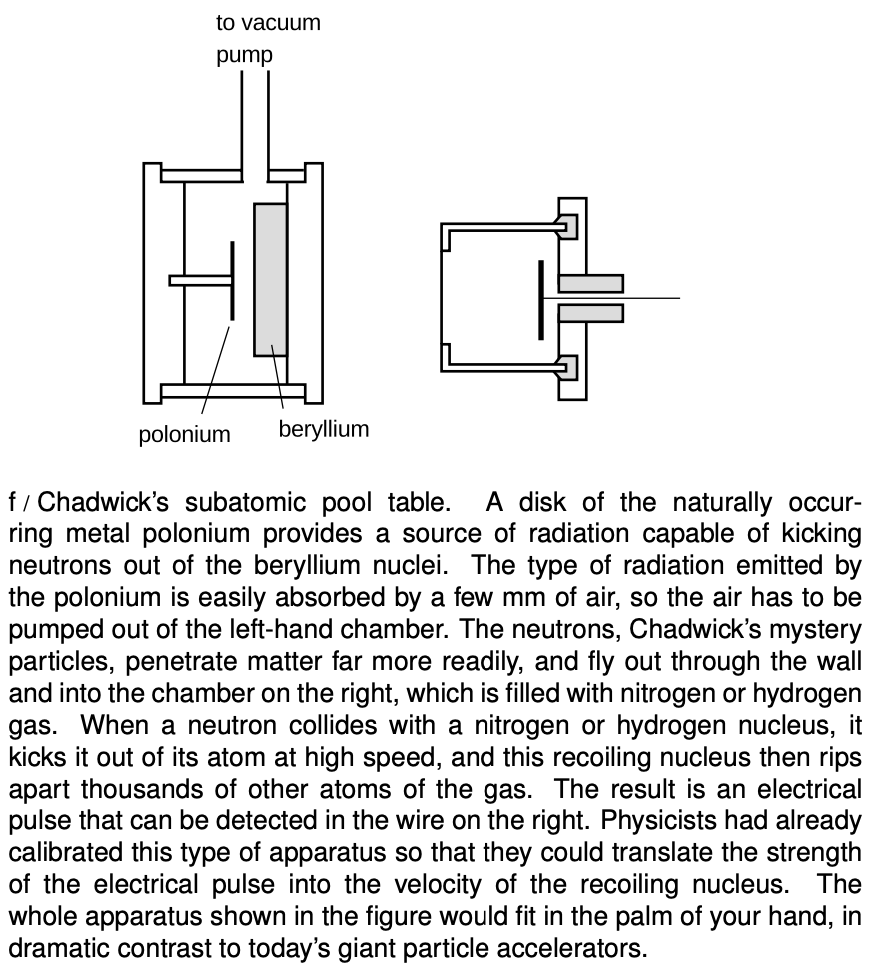
Suppose, for instance, that we bombard a sample of hydrogen atoms with the mystery particles. Since the participants in the collision are fundamental particles, there is no way for kinetic energy to be converted into heat or any other form of energy, and Chadwick thus had two equations in three unknowns:
equation #1: conservation of momentum
equation #2: no loss of kinetic energy
unknown #1: mass of the mystery particle
unknown #2: initial velocity of the mystery particle
unknown #3: final velocity of the mystery particle
The number of unknowns is greater than the number of equations, so there is no unique solution. But by creating collisions with nuclei of another element, nitrogen, he gained two more equations at the expense of only one more unknown:
equation #3: conservation of momentum in the new collision
equation #4: no loss of kinetic energy in the new collision
unknown #4: final velocity of the mystery particle in the new collision
He was thus able to solve for all the unknowns, including the mass of the mystery particle, which was indeed within 1% of the mass of a proton. He named the new particle the neutron, since it is electrically neutral.
Discussion Question
A Good pool players learn to make the cue ball spin, which can cause it not to stop dead in a head-on collision with a stationary ball. If this does not violate the laws of physics, what hidden assumption was there in the example above?
14.2 Collisions in one dimension by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.