15.2 Angular momentum in planetary motion by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
15.2 Angular momentum in planetary motion
We now discuss the application of conservation of angular momentum to planetary motion, both because of its intrinsic importance and because it is a good way to develop a visual intuition for angular momentum.
Kepler's law of equal areas states that the area swept out by a planet in a certain length of time is always the same. Angular momentum had not been invented in Kepler's time, and he did not even know the most basic physical facts about the forces at work. He thought of this law as an entirely empirical and unexpectedly simple way of summarizing his data, a rule that succeeded in describing and predicting how the planets sped up and slowed down in their elliptical paths. It is now fairly simple, however, to show that the equal area law amounts to a statement that the planet's angular momentum stays constant.
There is no simple geometrical rule for the area of a pie wedge cut out of an ellipse, but if we consider a very short time interval, as shown in figure i, the shaded shape swept out by the planet is very nearly a triangle. We do know how to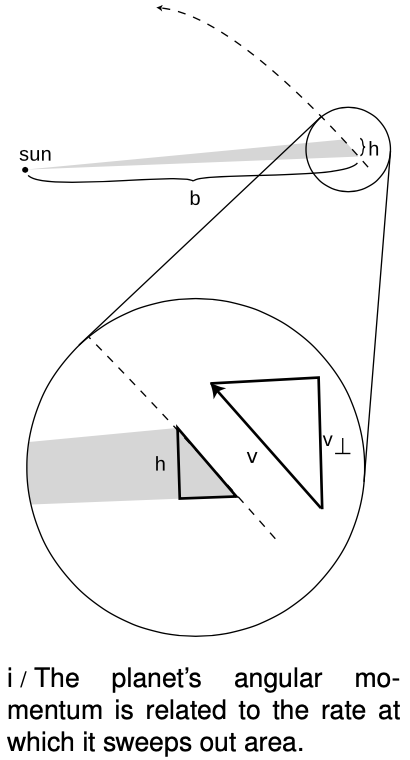 
compute the area of a triangle. It is one half the product of the base and the height:
We wish to relate this to angular momentum, which contains the variables `r` and `v_(bot)` . If we consider the sun to be the axis of rotation, then the variable `r` is identical to the base of the triangle, `r=b`. Referring to the magnified portion of the figure, `v_(bot)` can be related to `h`, because the two right triangles are similar:
`h/"distance traveled"=(v_(bot))/|v|`
The area can thus be rewritten as
`area=1/2r(v_(bot)"distance traveled")/|v|`.
The distance traveled equals `|v|Deltat`, so this simplifies to
`area=1/2rv_(bot)Deltat`.
We have found the following relationship between angular momentum and the rate at which area is swept out:
`L=2m(area)/(Deltat)`.
The factor of 2 in front is simply a matter of convention, since any conserved quantity would be an equally valid conserved quantity if you multiplied it by a constant. The factor of `m` was not relevant to Kepler, who did not know the planets' masses, and who was only describing the motion of one planet at a time.
We thus find that Kepler's equal-area law is equivalent to a statement that the planet's angular momentum remains constant. But wait, why should it remain constant? --- the planet is not a closed system, since it is being acted on by the sun's gravitational force. There are two valid answers. The first is that it is actually the total angular momentum of the sun plus the planet that is conserved. The sun, however, is millions of times more massive than the typical planet, so it accelerates very little in response to the planet's gravitational force. It is thus a good approximation to say that the sun doesn't move at all, so that no angular momentum is transferred between it and the planet.
The second answer is that to change the planet's angular momentum requires not just a force but a force applied in a certain way. In section 15.4 we discuss the transfer of angular momentum by a force, but the basic idea here is that a force directly in toward the axis does not change the angular momentum.
Discussion Questions
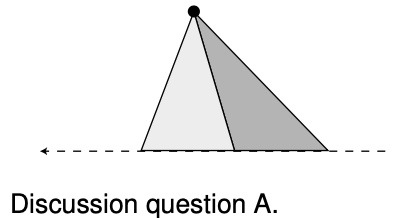A. Suppose an object is simply traveling in a straight line at constant speed. If we pick some point not on the line and call it the axis of rotation, is area swept out by the object at a constant rate? Would it matter if we chose a different axis?
B. The figure is a strobe photo of a pendulum bob, taken from underneath the pendulum looking straight up. The black string can't be seen in the photograph. The bob was given a slight sideways push when it was released, so it did not swing in a plane. The bright spot marks the center, i.e., the position the bob would have if it hung straight down at us. Does the bob's angular momentum appear to remain constant if we consider the center to be the axis of rotation? What if we choose a different axis?
15.2 Angular momentum in planetary motion by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.