Chapter 1 Scaling and estimation

1.1 Introduction

Why can't an insect be the size of a dog? Some skinny stretched-out cells in your spinal cord are a meter tall - why does nature display no single cells that are not just a meter tall, but a meter wide, and a meter thick as well? Believe it or not, these are questions that can be answered fairly easily without knowing much more about physics than you already do. The only mathematical technique you really need is the humble conversion, applied to area and volume.

Area and volume

Area can be defined by saying that we can copy the shape of interest onto graph paper with 1 cm ×
1 cm squares and count the number of squares inside. Fractions of squares can be estimated by eye. We then say the area equals the number of squares, in units of square cm. Although this might seem less “pure” than computing areas using formulae like `A=pi*r^2` for a circle or [Private Equation] for a triangle, those formulae are not useful as definitions of area because they cannot be applied to irregularly shaped areas.

Units of square cm are more commonly written as `"cm"^2`in science. Of course, the unit of measurement symbolized by “cm” is not an algebra symbol standing for a number that can be literally multiplied by itself. But it is advantageous to write the units of area that way and treat the units as if they were algebra symbols. For instance, if you have a rectangle with an area of `6"m"^2` and a width of `2` m, then calculating its length as `(6 "m"^2)"/"(2 "m")=3 "m"` gives a result that makes sense both numerically and in terms of units. This algebra-style treatment of the units also ensures that our methods of converting units work out correctly. For instance, if we accept the fraction `(100 "cm")/(1 "m")`as a valid way of writing the number one, then one times one equals one, so we should also say that one can be represented by `(100 "cm")/(1 "m")×(100 "cm")/(1 "m")`, which is the same as `(10000 "cm"^2)/(1 "m"^2)`.

That means the conversion factor from square meters to square centimeters is a factor of 10⁴, i.e., a square meter has 10⁴ square centimeters in it.

All of the above can be easily applied to volume as well, using one-cubic-centimeter blocks instead of squares on graph paper.

To many people, it seems hard to believe that a square meter equals 10000 square centimeters, or that a cubic meter equals a million cubic centimeters - they think it would make more sense if there were 100 cm² in 1 m², and 100 cm³ in 1 m³, but that would be incorrect. The examples shown in figure b aim to make the correct answer more believable, using the traditional U.S. units of feet and yards. (One foot is 12 inches, and one yard is three feet.)

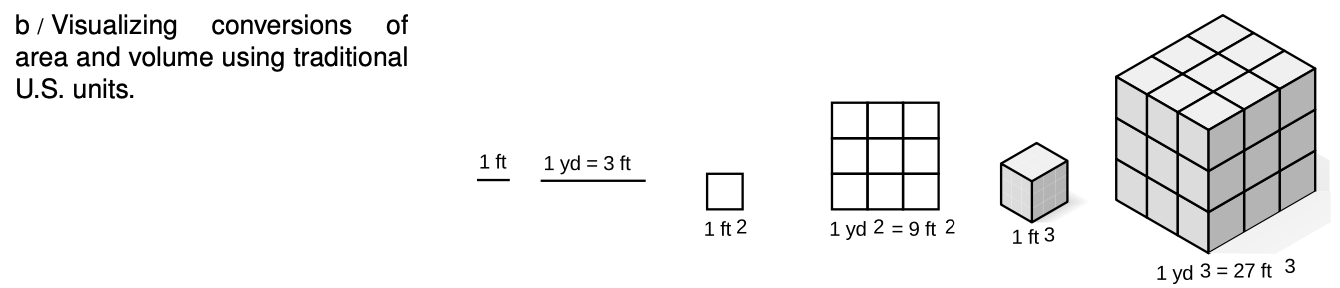
self-check: Based on figure b, convince yourself that there are `9 "ft"^2` in a square yard, and `27 "ft"^3`in a cubic yard, then demonstrate the same thing symbolically (i.e., with the method using fractions that equal one).
(answer in the back of the PDF version of the book)

`=>` Solved problem: converting `"mm"^2` to `"cm"^2` — problem 10

`=>` Solved problem: scaling a liter — problem 19

Discussion Question

A How many square centimeters are there in a square inch? (1 inch = 2.54 cm) First find an approximate answer by making a drawing, then derive the conversion factor more accurately using the symbolic method.

1.1 Introduction by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.