11.6 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
energy — A numerical scale used to measure the heat, motion, or other properties that would require fuel or physical effort to put into an object; a scalar quantity with units of joules (J).
power — The rate of transferring energy; a scalar quantity with units of watts (W).
kinetic energy — The energy an object possesses because of its motion.
heat — A form of energy that relates to temperature. Heat is different from temperature because an object with twice as much mass requires twice as much heat to increase its temperature by the same amount. Heat is measured in joules, temperature in degrees. (In standard terminology, there is another, finer distinction between heat and thermal energy, which is discussed below. In this book, I informally refer to both as heat.)
temperature — What a thermometer measures. Objects left in contact with each other tend to reach the same temperature. Cf. heat. As discussed in more detail in chapter 2, temperature is essentially a measure of the average kinetic energy per molecule.
Notation
`E` — energy
`J` — joules, the SI unit of energy
`KE` — kinetic energy
`P` — power
`W` — watts, the SI unit of power; equivalent to J/s
Other Notation
`Q` or `DeltaQ` — the amount of heat transferred into or out of an object
`K` or `T` — alternative symbols for kinetic energy, used in the scientific literature and in most advanced textbooks
thermal energy — Careful writers make a distinction between heat and thermal energy, but the distinction is often ignored in casual speech, even among physicists. Properly, thermal energy is used to mean the total amount of energy possessed by an object, while heat indicates the amount of thermal energy transferred in or out. The term heat is used in this book to include both meanings.
Summary
Heating an object, making it move faster, or increasing its distance from another object that is attracting it are all examples of things that would require fuel or physical effort. All these things can be quantified using a single scale of measurement, and we describe them all as forms of energy. The SI unit of energy is the Joule. The reason why energy is a useful and important quantity is that it is always conserved. That is, it cannot be created or destroyed but only transferred between objects or changed from one form to another. Conservation of energy is the most important and broadly applicable of all the laws of physics, more fundamental and general even than Newton's laws of motion.
Heating an object requires a certain amount of energy per degree of temperature and per unit mass, which depends on the substance of which the object consists. Heat and temperature are completely different things. Heat is a form of energy, and its SI unit is the joule (J). Temperature is not a measure of energy. Heating twice as much of something requires twice as much heat, but double the amount of a substance does not have double the temperature.
The energy that an object possesses because of its motion is called kinetic energy. Kinetic energy is related to the mass of the object and the magnitude of its velocity vector by the equation
Power is the rate at which energy is transformed from one form to another or transferred from one object to another,
`P=(DeltaE)/(Deltat)`. [only for constant power]
The SI unit of power is the watt (W).
Homework Problems
1. This problem is now problem 14 in chapter 12, on page 321.
2. Can kinetic energy ever be less than zero? Explain. [Based on a problem by Serway and Faughn.]
3. Estimate the kinetic energy of an Olympic sprinter.
4. You are driving your car, and you hit a brick wall head on, at full speed. The car has a mass of 1500 kg. The kinetic energy released is a measure of how much destruction will be done to the car and to your body. Calculate the energy released if you are traveling at (a) 40 mi/hr, and again (b) if you're going 80 mi/hr. What is counterintuitive about this, and what implication does this have for driving at high speeds? `sqrt`
5. A closed system can be a bad thing --- for an astronaut sealed inside a space suit, getting rid of body heat can be difficult. Suppose a 60-kg astronaut is performing vigorous physical activity, expending 200 W of power. If none of the heat can escape from her space suit, how long will it take before her body temperature rises by 6°C (11°F), an amount sufficient to kill her? Assume that the amount of heat required to raise her body temperature by 1°C is the same as it would be for an equal mass of water. Express your answer in units of minutes. `sqrt`
6. All stars, including our sun, show variations in their light output to some degree. Some stars vary their brightness by a factor of two or even more, but our sun has remained relatively steady during the hundred years or so that accurate data have been collected. Nevertheless, it is possible that climate variations such as ice ages are related to long-term irregularities in the sun's light output. If the sun was to increase its light output even slightly, it could melt enough Antarctic ice to flood all the world's coastal cities. The total sunlight that falls on Antarctica amounts to about `1×10^16` watts. In the absence of natural or human-caused climate change, this heat input to the poles is balanced by the loss of heat via winds, ocean currents, and emission of infrared light, so that there is no net melting or freezing of ice at the poles from year to year. Suppose that the sun changes its light output by some small percentage, but there is no change in the rate of heat loss by the polar caps. Estimate the percentage by which the sun's light output would have to increase in order to melt enough ice to raise the level of the oceans by 10 meters over a period of 10 years. (This would be enough to flood New York, London, and many other cities.) Melting 1 kg of ice requires `3×10^3 J`.
7. A bullet flies through the air, passes through a paperback book, and then continues to fly through the air beyond the book. When is there a force? When is there energy? (solution in the pdf version of the book)
8. Experiments show that the power consumed by a boat's engine is approximately proportional to the third power of its speed. (We assume that it is moving at constant speed.) (a) When a boat is crusing at constant speed, what type of energy transformation do you think is being performed? (b) If you upgrade to a motor with double the power, by what factor is your boat's crusing speed increased? [Based on a problem by Arnold Arons.] (solution in the pdf version of the book)
9. Object A has a kinetic energy of 13.4 J. Object B has a mass that is greater by a factor of 3.77, but is moving more slowly by a factor of 2.34. What is object B's kinetic energy? [Based on a problem by Arnold Arons.] (solution in the pdf version of the book)
10. The moon doesn't really just orbit the Earth. By Newton's third law, the moon's gravitational force on the earth is the same as the earth's force on the moon, and the earth must respond to the moon's force by accelerating. If we consider the earth and moon in isolation and ignore outside forces, then Newton's first law says their common center of mass doesn't accelerate, i.e., the earth wobbles around the center of mass of the earth-moon system once per month, and the moon also orbits around this point. The moon's mass is 81 times smaller than the earth's. Compare the kinetic energies of the earth and moon. (We know that the center of mass is a kind of balance point, so it must be closer to the earth than to the moon. In fact, the distance from the earth to the center of mass is 1/81 of the distance from the moon to the center of mass, which makes sense intuitively, and can be proved rigorously using the equation on page 366.)
11. My 1.25 kW microwave oven takes 126 seconds to bring 250 g of water from room temperature to a boil. What percentage of the power is being wasted? Where might the rest of the energy be going? (solution in the pdf version of the book)
12. The multiflash photograph shows a collision between two pool balls. The ball that was initially at rest shows up as a dark image in its initial position, because its image was exposed several times before it was struck and began moving. By making measurements on the figure, determine numerically whether or not energy appears to have been conserved in the collision. What systematic effects would limit the accuracy of your test? [From an example in PSSC Physics.]
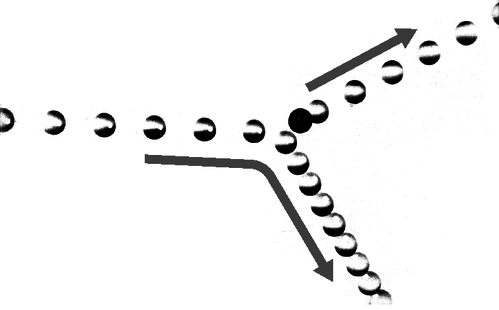
g / Problem 12.
13. This problem is a numerical example of the imaginary experiment discussed on p. 298 regarding the relationship between energy and relative motion. Let's say that the pool balls both have masses of 1.00 kg. Suppose that in the frame of reference of the pool table, the cue ball moves at a speed of 1.00 m/s toward the eight ball, which is initially at rest. The collision is head-on, and as you can verify for yourself the next time you're playing pool, the result of such a collision is that the incoming ball stops dead and the ball that was struck takes off with the same speed originally possessed by the incoming ball. (This is actually a bit of an idealization. To keep things simple, we're ignoring the spin of the balls, and we assume that no energy is liberated by the collision as heat or sound.) (a) Calculate the total initial kinetic energy and the total final kinetic energy, and verify that they are equal. (b) Now carry out the whole calculation again in the frame of reference that is moving in the same direction that the cue ball was initially moving, but at a speed of 0.50 m/s. In this frame of reference, both balls have nonzero initial and final velocities, which are different from what they were in the table's frame. [See also problem 15 on p. 382.]
14. One theory about the destruction of the space shuttle Columbia in 2003 is that one of its wings had been damaged on liftoff by a chunk of foam insulation that fell off of one of its external fuel tanks. The New York Times reported on June 5, 2003, that NASA engineers had recreated the impact to see if it would damage a mock-up of the shuttle's wing. “Before last week's test, many engineers at NASA said they thought lightweight foam could not harm the seemingly tough composite panels, and privately predicted that the foam would bounce off harmlessly, like a Nerf ball.” In fact, the 1.7-pound piece of foam, moving at 531 miles per hour, did serious damage. A member of the board investigating the disaster said this demonstrated that “people's intuitive sense of physics is sometimes way off.” (a) Compute the kinetic energy of the foam, and (b) compare with the energy of a 170-pound boulder moving at 5.3 miles per hour (the speed it would have if you dropped it from about knee-level).
(c) The boulder is a hundred times more massive, but its speed is a hundred times smaller, so what's counterintuitive about your results? `sqrt`
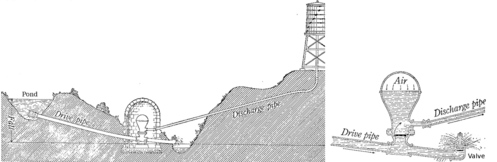
15. The figure above is from a classic 1920 physics textbook by Millikan and Gale. It represents a method for raising the water from the pond up to the water tower, at a higher level, without using a pump. Water is allowed into the drive pipe, and once it is flowing fast enough, it forces the valve at the bottom closed. Explain how this works in terms of conservation of mass and energy. (Cf. example 1 on page 289.)
16. The following table gives the amount of energy required in order to heat, melt, or boil a gram of water.
| heat 1 g of ice by 1°C | 2.05 J |
| melt 1 g of ice | 333 J |
| heat 1 g of liquid by 1°C | 4.19 J |
| boil 1 g of water | 2500 J |
| heat 1 g of steam by 1°C | 2.01 J |
(a) How much energy is required in order to convert 1.00 g of ice at -20 `°C` into steam at 137 `°C`? `sqrt`
(b) What is the minimum amount of hot water that could melt 1.00 g of ice? `sqrt`
17. Estimate the kinetic energy of a buzzing fly's wing. (You may wish to review section 1.4 on order-of-magnitude estimates.)
18. A blade of grass moves upward as it grows. Estimate its kinetic energy. (You may wish to review section 1.4 on order-of-magnitude estimates.)
11.6 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.