The Lens Maker's Calculator uses the Lens Maker Equation1 to calculate the focal length of a thin lens in air (or some other medium). The Lens Maker's Equation assumes thin lenses; it ignores the width of the lens and assumes that the light immediately goes from one side to the other. This, of course, isn't what actually happens, but it's a reasonable assumption in certain situations, such as very thin lenses.
`f = [(n_"lens"/n_"medium" - 1)(1/r_1 - 1/r_2)]^-1`
where:
- f is the focal length of the lens
- nlens is the index of refraction of the lens. For more information on the index of refraction, click here.
- nmedium is the index of refraction of the material surrounding the lens.
- r1 is the radius of lens curvature of the side nearest the "object" ( the source of the light rays).
- r2 is the radius of lens curvature of the side farthest from the object.
Radius of Curvature
The radius of curvature can be positive or negative, depending on which way it curves and where it's facing 2. When a convex surface faces the object, we say its radius of curvature is positive. When a concave surface faces the object, we say its radius is negative. If the surface is facing away from the object, then we simply use the opposite sign of if the surface faced the object.
Lens Curvature
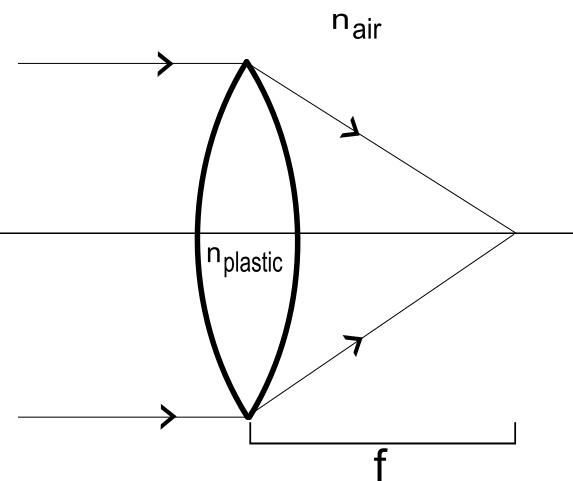
If a lens curves outward, it's said to be convex (see Pictures 1 and 3). If a lens bows inwards, it's said to be concave (see Picture 2). If a lens curves out on one side and in on the other, then it's called convex-concave, or concave-convex, depending on the orientation. See Pictures 4 and 5.
Focal Length
The focal length is the distance along the optical axis between the focal point and the lens. Basically, it's the distance between the center of the lens and the point where the lens focuses light. Conventionally, we set up lens diagrams with light going left to right, where distance to the left of the lens is negative and distance to the right of the lens is positive. In this set up, a positive focal length means that the light rays will be bent by the lens so that they intersect on the right side of the lens. A focal length of 10 cm means that the light rays will be most focused 10 cm past the lens. See Picture 1. Lenses with a positive focal length are said to be converging because they bend the light rays toward each other.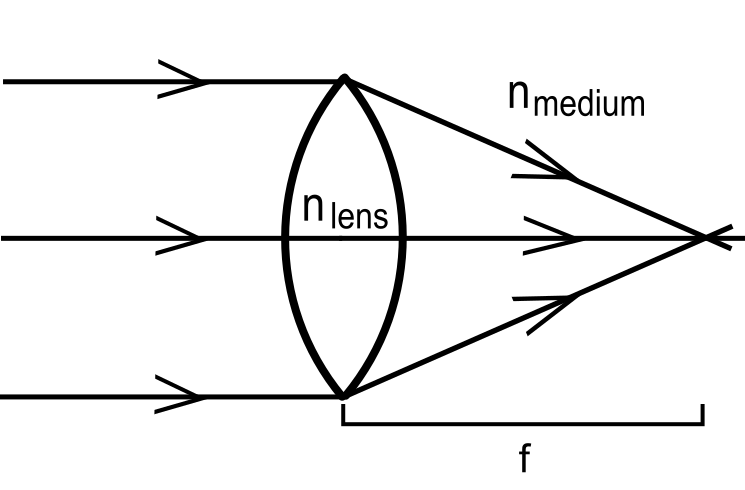
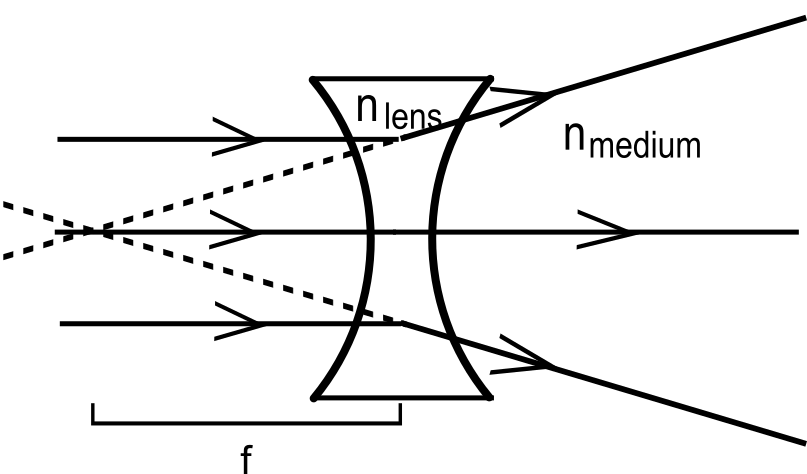

If the focal length is negative, then the light rays exiting the lens will have been bent in such a way that they look as if they intersected behind the lens (to the left in the pictures). The light rays never actually crossed in this way, but it will appear like they did to the observer in front of the lens. See picture 2. Lenses with a negative focal length are said to be diverging because they bend the light rays away from each other.
Examples
See Picture 3. Let's say that the lens is plastic, so `n_"lens" approx 1.5`, and it's surrounded by air, `n_"medium" approx 1`. Both sides of the lens are convex. Generally, we arrange the lens so that the object is on the left side. Therefore, `r_1` is positive and `r_2` is negative. Let's say that the magnitude of each radius of curvature is 2. If we plug this into the lens maker's equation:
- `f = [( 1.5/1 - 1) (1/2 - 1/-2)]^(-1) `
- `[.5 * 1]^(-1) `
- =` 1/.5 = 2`
See picture 4. Let's use the same indices and magnitudes, but this time the right side of the lens is concave. A concave surface facing away from the object has a positive radius of curvature, so the lens maker's equation says:
- `f = [(1.5/1 -1) (1/2 - 1/2)]^(-1)`
- = `[1/2 * 0]^(-1)`
- = `[0]^(-1)`
Here's an interesting situation: because of the geometry of this lens `(|r_1| = |r_2|`, along with other factors`)`, we see that `f = [0]^(-1)`. A rigorous mathematical approach to this situation would probably involve limits, but in physics we tend to be a little more casual about this when possible: `f = 1/0 = infty`. An infinite focal distance means that the rays leaving the lens are parallel.
This equation assumes a thin lens, so the lines aren't shown to move vertically. However, a more robust approach to this situation would find that the lines are shifted in towards the middle, something like Picture 5.