Determinant of a 2x2 Matrix

The Determinant of a 2x2 Matrix calculator computes the determinant of a 2x2 matrix.

INSTRUCTIONS: Enter the following:

• (A) This is the 2x2 matrix

Determinant:  The calculator returns the determinant of the 2x2 matrix.

The Math

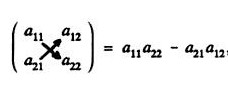
The determinant of a 2x2 matrix

`A = ((a, b), (c, d))`

is the number ad -bc. It is denoted det A. 

It is important to note that matrices whose determinants are equal to zero are referred to as singular or degenerate matrices. Matrices whose determinants are not zero are referred to as non-singular. Given a matrix A where det A `!=` 0, the only equilibrium point for the linear system `frac(d bb "Y")(dt)` = `bb "AY"` is the origin. 

Blanchard, Devaney, and Hall note the example (242): 

`A = ((2, 1), (-4, 0.3))`

det A = (2)(0.3)-(1)(-4)= 4.6. Since det A `!=` 0, the only equilibrium point for this system is the origin (0, 0).

Blanchard, Paul, Robert L. Devaney, and Glen R. Hall. Differential Equations. 3rd ed. Belmont, CA: Thomson Brooks/Cole, 2006. Print. 

2x2 Matrix Calculators :

• To compute the Characteristic Polynomial of a 3x3 matrix,CLICK HERE.
• To compute the Trace of a 2x2 Matrix, CLICK HERE.
• To compute the Inverse of a 2x2 Matrix, CLICK HERE.
• To compute the Eigenvalues of a 2x2 Matrix, CLICK HERE.
• For the Classifying Equilibria of a 2x2 Matrix, CLICK HERE.
• To compute the Eigenvalues and Eigenvectors of a 2x2 Matrix, CLICK HERE.
• To multiply a 2x2 matrix by a scalar, CLICK HERE.
• To compute the Characteristic Polynomial of a 2x2 Matrix, CLICK HERE.