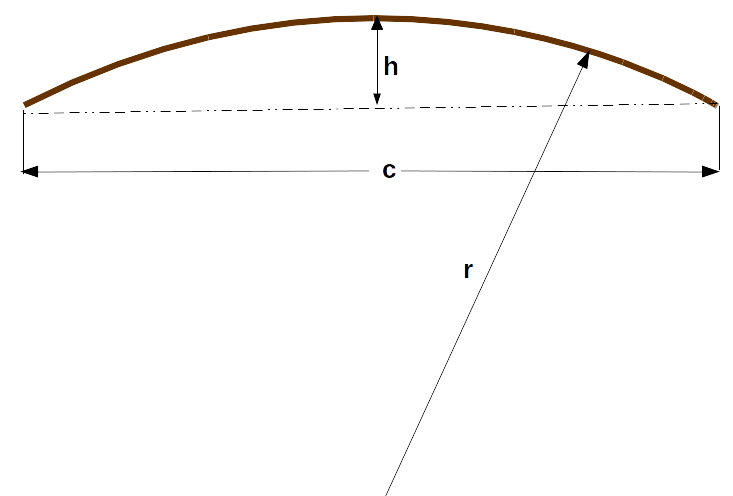
The Radius of an Arch calculator computes the radius (r) of a circle that would trace an arc of a certain chord length (c) and at a certain height (h).
INSTRUCTIONS: Choose units and enter the following:
- (c) Length of Chord (see diagram)
- (h) Height of Arc from Chord to Highest Point
Radius of Arch (r): The calculator returns the radius is in inches. However, this can be automatically converted to numerous other length units (e.g. centimeters or yards) via the pull-down menu.
The Math / Science
The Radius of an Arch calculator computes the radius of a circle that can be used to mark an arch based on the cord length of the arch and the height of the arch. Arches on buildings and arched railings can be built using this formula. The following is a video (YouTube) that shows the use of this equation to build an arched railing on a porch. CLICK HERE. This can also be used to trace lines for painted arches as in the photograph of arches painted on a barn door (Special thanks to my friend Austin).
The formula for the Radius of an Arch is:
`r = c^2 / (8*h) + h/2`
where:
- r = radius of arch
- c = arch chord length
- h = height of arch
HOW TO GUIDE
 Arches Painted on Barn Door
Arches Painted on Barn Door
Let's use my neighbor's sliding barn doors as our working example. But you'll see that it works for any application.
- First, measure how wide you want your arch. This is the Length of the Chord (c) in the diagram, but it's the width of the white sections in the barn door way.
- Then, choose the drop you want from the apex. This is (h) in the diagram. On the doorway, it looks like the drop is about a foot.
- With these measurements, you can use this calculator to compute the radius (r) of the circle that will be your guide.
- Next, cut a piece of string or mark the string on a plumb-bob to the length of the radius (r).
- Then, calculate and measure where the mid-point from the ends of your arch.
- Then go to the apex of where you want the arch, at the highest point in the middle and lower your string straight down. This is where the plumb-bob works well. The bottom of the string will mark your center point of the circle; mark it.
- Then attach the end of your string to that center point with a tack or screw.
- Then extend the string and let it work as a compass for you to draw your arc from side to side.
Viola! You're done. You now have a perfectly rounded arch drawn on your material, and you can paint or cut with precision.
Circle Calculators
- Circle Area - Computes the area of a circle given the radius (A = π r2).
- Area of Circle Arc Segment f(r,θ) - Computes the area of an arc segment of a circle given the radius (r) and angle (θ)
- Area of Circle Arc Segment Area f(r,h) - Computes the area of an arc segment of a circle given radius (r) and the depth (h) into the circle.
- Area of Circle Sector f(r,Θ) - Computes the area of a sector (pie slice) of a circle given the radius (r) and angle (Θ).
- Angle of Circle Sector f(r,h) - Computes the angle in a circle from the radius and depth of the chord.
- Area of Circle Annulus - Computes the area of an annulus (ring) given the inner radius (r) and outer radius (R).
- Radius of Circle from Center and a Point - Computes the radius of a circle given the center point (h,k) and any other point (x,y) on the circle.
- Circumference of Circle - Computes the circumference of a circle given the radius (C = 2 π r).
- Circle Arc Length - Computes the length of an arc length on a circle given the radius (r) and angle (Θ)
- Circle within a Triangle - Computes the radius of a circle inscribed within a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle around a Triangle - Computes the radius of a circle that circumscribes a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle Radius from Circumference - Computes the radius of a circle given the circumference.
- Circle Circumference from Area - Computes the circumference of a circle given the area.
- Circle Radius from Area - Computes the radius of a circle given the area.
- Circle Radius from Chord - Computes the radius of a circle based on the length of a chord and the chord's center height.
