Area is the quantity that expresses the extent of a two dimensional figure or shape, or planar lamina, in the plane. surface area is its analog on the two-dimensional surface of a three dimensional surface. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid(a three-dimensional concept).
The area of a shape can be measured by comparing the shape to squares of a fixed size. the standard unit of area is the square metre (written as m2), which is the area of a square whose sides are one metrelong.A shape with an area of three square metres would have the same area as three such squares.
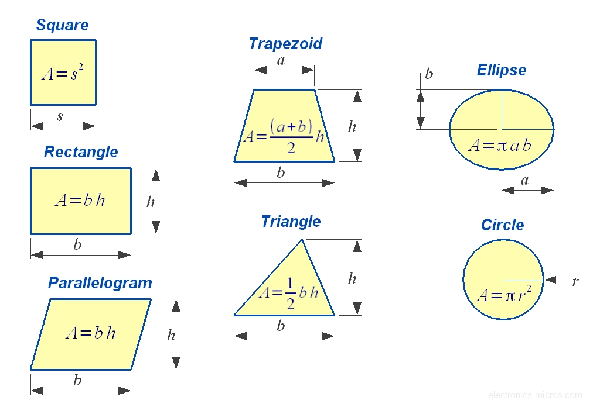
There are several well-known formulas for the areas of simple shapes such as triangles, rectangles, and circles.
For a solid shape such as a sphere, cone, or clinder, the area of its boundary surface is called the surface area. Formulas for the surface areas of simple shapes were computed by the ancient Greeks, but computing the surface area of a more complicated shape usually requires multivariable calculus.
Area plays an important role in modern mathematics. In addition to its obvious importance in geometry and calculus, area is related to the definition of determinants in linear algebra, and is a basic property of surfaces in differential geometry.In analysis, the area of a subset of the plane is defined using lebesgue measurement,though not every subset is measurable.In general, area in higher mathematics is seen as a special case of volume for two-dimensional regions.
Area can be defined through the use of axioms, defining it as a function of a collection of certain plane figures to the set of real numbers. It can be proved that such a function exists.