The Two Pulley Belt Length equation computes the length of a belt that goes around two pulleys, where the pulleys may be of unequal radii.
INSTRUCTIONS: Choose your preferrred units and enter the following:
- (R) The radius of the larger pulley
- (r) The radius of the smaller pulley
- (L) The distance between the axles
Belt Length: The calculator returns the belt length in inches. However, this can be automatically converted to other length units via the pull-down menu.
See the video explanation of this equation's derivation.
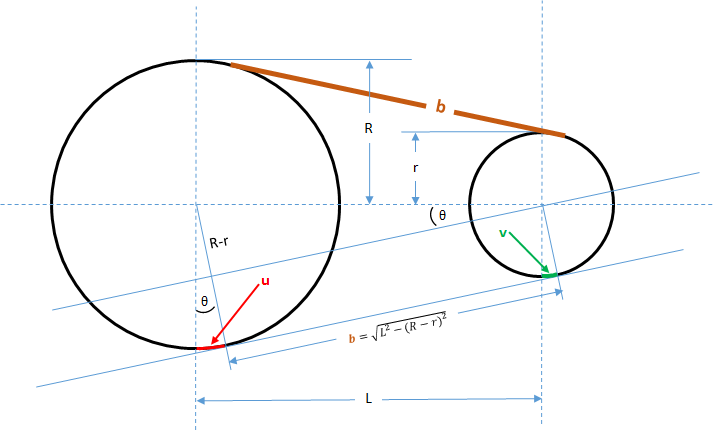
Notes
From the picture, see that the following describe the component parts of the solution:
`C_R` = half the larger pulley circumference = `pi / 2 * 2R`, where 2R = larger pulley diameter
`C_r` = half the smaller pulley circumference = `pi / 2 * 2r`, where 2r = larger pulley diameter
u = segment of larger circumference between half circle and tangent point of pulley = `theta/(2pi) * (pi * 2R)`
v = segment of smaller circumference between half circle and tangent point of pulley = `theta/(2pi) * (pi * 2r)`
b = length of belt between tangent point on two pulleys = `sqrt( L^2 - (R-r)^2 )`
`L * sin( theta ) = R - r` ` =>` `theta = asin( (R-r)/L )`
Belt Length = (`C_R + 2u`) + (`C_r - 2v`) + 2b
= (`piR + 2* thetaR`) + (`pir - 2* thetar`) +2b
= `pi ( R+r) + 2theta* (R-r) + 2b`
= `pi ( R+r) + 2* asin( (R-r) / L) * (R-r) + 2*sqrt( L^2 - (R-r)^2)`