The Rotational Speed at Latitude calculator computes the rotational speed on the surface of the Earth based on the Earth's Rotation Rate and the latitude.

INSTRUCTIONS: Enter the following:

• (α)  Latitude (Latitude goes from 0 degrees at the equator to 90 degrees at either the North Pole or the South Pole). 

Rotational Speed (S): The calculator returns the Rotational Speed in miles per hour.   However, this can be automatically converted to other velocity units (e.g. meters per second or kilometers per hour). 

Note: to convert from Degrees, Minutes and Seconds to Decimal Degrees, CLICK HERE.

The Math / Science

The rotation rate of the Earth is constant.  However, one's distance from the polar axis is a function of latitude.  Based on one's latitude, the rotational speed can be computed.  Note: latitude can be either north or south, but the effect on the rotational speed is the same.   The formula for the Rotational Speed at Latitude is:

        s = 2π•Re•cos(α)/Sd

where:

• s is the rotational speed at a latitude on Earth
• Re is the equatorial radius of the Earth
• α is the latitude
• Sd is the duration of a sidereal day

How fast are you really moving?

This equation computes the rotational speed (S) of a point on the Earth defined by its latitude (`alpha`).  This equation assumes a round Earth approximation and uses the WGS-84 value for the .

DERIVATION

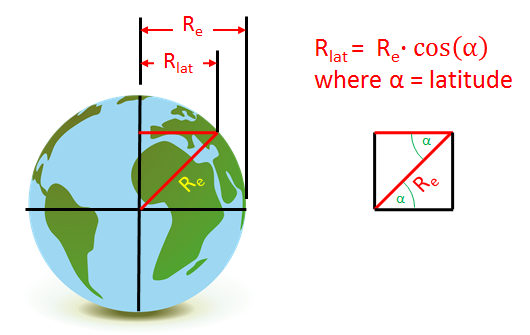
First we recognize the circle that is the equator and the circle created by the rotation of a point on the Earth at a non-zero latitude describe circles in parallel planes.  Thus the radius of that circle at a specified latitude and the radius at the equator can be rotated in those parallel planes to be parallel lines -- as drawn in the figure at the left.  The black line at the equator is parallel to the red radius of dimension R_lat.

These two radii crossed by the radius drawn diagonal from the center of the Earth to the specified latitude, form two internal opposite angles, `alpha`.  We know from basic geometry that the two internal angles (`alpha`) in the figure are equal.  The top red line of the triangle is then the cosine of the angle, `alpha`, multiplied by the length of the right triangle's hypotenuse:

R_lat = R_e•cos(α)   where R_e is 6378137.0 m

Next, knowing the circumference of the circle whose radius is R_lat is given by Circumference = 2•π•R_lat we have the distance a point rotates each day at the latitude given by `alpha`.

Then we can compute the instantaneous velocity of a point on the globe at the specified latitude, α, by dividing the distance traveled in one day (in one rotation of the globe) by the number of hours in a sidereal day ( 23.9344699 hours).  A sidereal day is the true period of a 360 degree rotation of the Earth in space.  This takes into account the difference in from solar day attributed to the Earth's flight around the Sun.

Examples

• If we enter the latitude of Columbus, Ohio (39.961176 degrees) -- home to THE Ohio State University -- we find the rotational speed of the horseshoe stadium is approximately 795.3 mph. So, when a Buckeye fan is shouting O - H, their seat is moving at a pretty good speed.
• If we enter the latitude 0 degrees to determine the rotational speed at the equator, we find the rotational speed of a point at the equator is approximately 1037.6 mph.
• If we enter the latitude of London England (about 51.533 degrees), we find the rotational speed of the London Bridge is approximately 645.4 mph.
• If we enter the latitude of Anchorage, Alaska (about 54.667 degrees), we find that city has a rotational speed of approximately 600 mph.
• If we enter the latitude of Reykjavík, Iceland (64.0667 degrees), we find that capital has a rotational speed of approximately 453.8 mph.