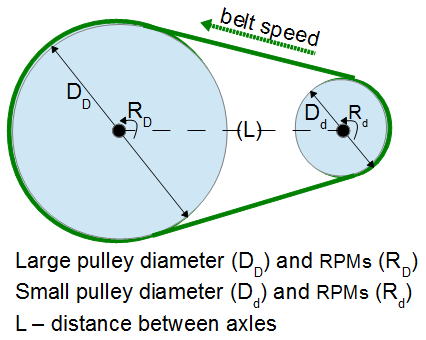
This Pulley Geometry Exercise equation computes the circumference of a shape that is analogous to a belt that encircles two pulleys of different sizes. This is an interesting formula to construct because of the basic geometric shapes and their relatively simple combination. See the equation Two Pulley Belt Length for a practical application of the geometry exercise discussed here.
If you're interested in a full explanation of the derivation of this equation, see the video explanation of this geometry exercise. It is 19 minutes long so does examine all the geometry applied.
INPUTS
The inputs to this equation are:
- the radius of the larger circular element, R
- the radius of the smaller circular, r
- the distance between the circle centers, L
Simple Machine Calculators
 Two and Three pulley systems
Two and Three pulley systems
- Lever Beam Length
- Leverage Lift Weight
- Fulcrum Position
- Belt Length
- Belt Speed.
- Pulley RPMs
- 2nd Pulley RPMs
- 2nd Pulley Diameter
- RPM of 4th pulley on three shafts
- 2nd Gear RPM
DERIVATION
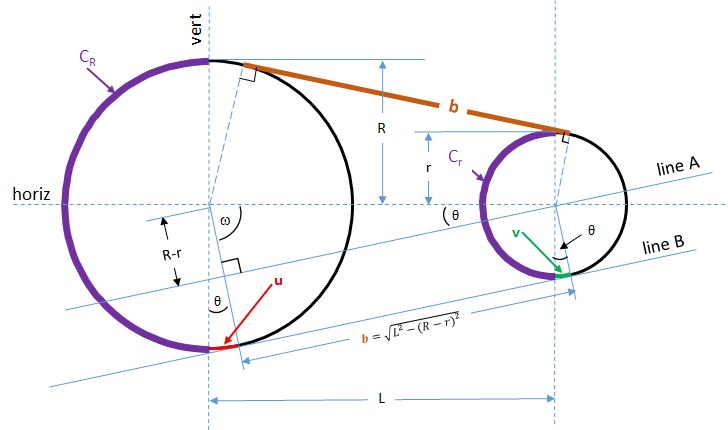
Let's walk through the steps of building this equation which computes the length of the pulley that would encompass two circles with different radii. There are a number of general geometric principles represented here which makes this a quite interesting problem of combining simple geometries.
THE COMPONENT PIECES OF THE GEOMETRY
From the picture, see first that the following describe the component parts of the solution:
- `C_R` = half the larger pulley circumference = `pi / 2 * 2R`, where 2R = larger pulley diameter `=>` `C_R = pi *R`
- `C_r` = half the smaller pulley circumference = `pi / 2 * 2r`, where 2r = larger pulley diameter
- u = segment of larger circle's circumference between half circle and tangent point to the larger circle
- v = segment of smaller circumference overlapping half circle at the tangent point to the smaller circle
- b = length of belt between tangent point on two pulleys = `sqrt( L^2 - (R-r)^2 )`
- L = the separation distance between the two circle's centers.
Because of the geometry we are defining as a belt wrapped around two circles, the line segment , b, touches both circles at a tangent point.
BUILDING THE EQUATIONS MODEL FROM SCRATCH
To start building this equation, we first note that the belt wraps around both circles and the last point the belt touches on either circle is a tangent point to the circle. In other words the belt stops touching the circle at the point of very last intersection point with the circle and thus the line segment b is tangent to the circle at that point. We also know that means the radial line to that same point where the belt last touches the tangent point of the circle is by definition perpendicular to the line touching that single point on the circle.
Since the line segment, b, by the belt definition is tangent to both circles, the radial lines of both circles intersect the tangent at right angles. This makes the two radial lines parallel, the smaller circle's radial line to the belt tangent point and the larger circle's radial line to the belt tangent point.
Therefore the two radial lines to the belt tangent points on the two circles are parallel. That makes the angle between the radial lines at the belt tangent points and the perpendicular lines through the circle centers equal angles. The equal angles are labeled `theta`.
The angle, `theta` just described, defines the arc lengths u and v. Twice arc length u must be added to `C_R` to define the length of the belt wrapped around (touching the larger circle. Similarly, twice the arc length v must be subtracted from `C_r` to define the length of belts wrapped around the smaller circle. So, we must derive the value of `theta` based on input variables to then determine the arc lengths u and v.
Since the horizontal and vertical lines through the center of the larger circle form a right angle, angle `omega` = 90 - `theta`. That, in turn, defines the angle between the horizontal and line A to also be equal to `theta'. So, `L * sin( theta ) = R - r` ` =>` `theta = asin( (R-r)/L )`.
Now that we know `theta` in terms of input variables, we can compute arc segment u and v.
`u = theta/(2pi) * (pi * 2R) => u = theta * R`
`v = theta/(2pi) * (pi * 2r) => u = theta * r`
Using the fact that the triangle labeled with angles `omega` and `theta` is also a right angle, we know `b = sqrt(L^2 - (R-r)^2)`
Belt Length = (`C_R + 2u`) + (`C_r - 2v`) + 2b
= (`pi*R + 2* theta*R`) + (`pi*r - 2* theta*r`) +2b
= `pi ( R+r) + 2theta * (R-r) + 2b`
= `pi ( R+r) + 2* asin( (R-r) / L) * (R-r) + 2*sqrt( L^2 - (R-r)^2)`