Processing...
`dotomega_"J2" = 0.75 * "n" *J_2 (R_E/ "a" )^2 * (4 - 5 sin^2(i)) / (1-e^2)^2`
Enter a value for all fields
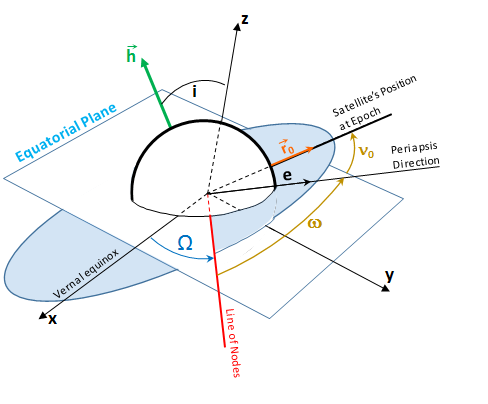
The Non-Spherical Earth perturbation equation for the rate of change of the argument of perigee, `dotomega`, of an orbit where the rate of change (`dotomega_"J2"`) in deg/day results from the `J_2` geopotential coefficients derived from the geopotential function of the Earth. The inputs to this equation are:
- the mean motion of the orbit (n) in deg/day
- the Earth equatorial radius (`R_E`) in kilometers
- the orbit's semi-major axis (a) in kilometers
- the eccentricity of the orbit, (e)
- the orbit inclination (i)
Notes
The earth is not a sphere. In fact, the Earth is neither a homogeneous mass nor a sphere. Consequently, the several attributes of the Earth's shape and composition have noticeable affects on a satellite's orbit. The bulge at the equator, the flattening at the poles, and the slight pear shape of the Earth are important contributors to the perturbation of an orbit due to a non-spherical Earth.