The Centroid of a Beam Section calculator computes the y-centroid (y being vertical axis of an I-beam's cross-section). 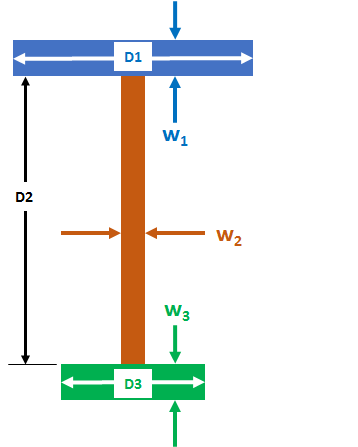
INSTRUCTIONS: Choose units and enter the following:
- (D1) Top width
- (W1) Top thickness
- (W2) Vertical thickness
- (D2) Interior height
- (D3) Bottom width
- (W3) Bottom thickness
y-centroid (y): The calculator return the centroid in millimeters. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The Centroid of a Beam Section calculator computes the y-centroid (y being vertical axis of an I-beam's cross-section). The centroid is the center of mass of the beam's cross-sectional sections. The centroid is used to compute the moment of inertia of the beam, which is used in analysis of the beam's bending stress under weight, beam shear, and beam deflection or other analysis questions.
We split the cross-section into into three segments, each segment having a nice rectangular symmetry. We then calculate the area and y-centroid of each of the three segments and compute the entire centroid as:
`bary = sum(A_i*y_i)/(sum A_i)`
The three segments are shown in the figure below, where `A_i = w_i *D_i`:
And the y-centroids of the segments are given as:
- `y_1 = w_3 +D_2 + w_1/2`
- `y_2 = w_3 +D_2/2`
- `y_3 = w_3/2`