The Apsis calculator has the following functions: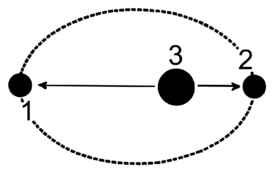
The apsides indicate the nearest
and furthest points of an
orbiting body around its host.
(1) farthest - apocenter
(2) nearest - pericenter
(3) focus - primary
- Apsis-Apocenter (minimum speed) computes the minimum velocity at the maximum distance of an orbit.
- Apsis-Apocenter (maximum distance) computes the greatest distance from the center of gravity in an orbit.
- Apsis-Pericenter (maximum speed) computes maximum velocity at the minimum distance of an orbit.
- Apsis-Pericenter (minimum distance) computes the minimum distance from the center of mass in an orbit.
- Standard Gravitational Parameter
- Force of Gravity computes the force of gravity between two bodies.
- Universal Gravity Constant
The Math / Science
An apsis is an extreme point in the orbit of an object. For elliptic orbits about a larger body, there are two apsides, named with the prefixes peri- (meaning 'near') and ap-/apo- (meaning 'away from') added to a reference to the body being orbited.
- For a body orbiting the Sun, the point of least distance is the perihelion, and the point of greatest distance is the aphelion
The terms become periastron and apastron when discussing orbits around other stars. - For any satellite of Earth, including the Moon, the point of least distance is the perigee and greatest distance the apogee.
- For objects in lunar orbit, the point of least distance is the pericynthion (/ˌpɛrɪˈsɪnθiən/) and the greatest distance the apocynthion. Perilune and apolune are also used.
- For an orbit around any barycenter, the terms periapsis and apoapsis (or apapsis) are used. Pericenter and apocenter are equivalent alternatives.
A straight line connecting the periapsis and apoapsis is the line of apsides. This is the major axis of the ellipse, its greatest diameter. The center of mass, or barycenter, of a two-body system lies on this line at one of the two foci of the ellipse. When one body is sufficiently larger than the other, this focus may be located within the larger body. However, whether this is the case, both bodies are in similar elliptical orbits. Both orbits share a common focus at the system's barycenter, with their respective lines of apsides being of length inversely proportional to their masses.
In orbital mechanics, the apsis technically refers to the distance measured between the barycenters of the central body and orbiting body. However, in the case of spacecraft, the family of terms are commonly used to refer to the orbital altitude of the spacecraft from the surface of the central body (assuming a constant, standard reference radius).
The Force of Gravity equation is:
F = (G•m1•m2)/D²
where:
- F is the force of gravity
- G is the Universal Gravitational Constant is 6.67384E-11 m³/kg•sec².
- m1 is the mass of the first object
- m2 is the mass of the second object
- D is the distance between them.
The formula for the Apsis-Pericenter maximum speed is:
`v_(per) = sqrt ( ((1+e)mu)/((1-e)a) ) `
where:
- vper is velocity at perigee
- e = eccentricity
- a = semi-major axis
- μ = standard gravitational parameter (μ = M•G)
The formula for the Apsis-Apocenter maximum distance is:
rap=(1+e)a
where:
- rap is distance at apogee
- e = eccentricity
- a = semi-major axis
The formula for the Apsis-Pericenter maximum speed is:
`v_(per) = sqrt ( ((1+e)mu)/((1-e)a) ) `
where:
- vper is velocity at perigee
- e = eccentricity
- a = semi-major axis
- μ = standard gravitational parameter (μ = M•G)
The formula for the Apsis-Pericenter minimum distance is:
rper=(1-e)a
where:
- rper is distance at perigee
- e = eccentricity
- a = semi-major axis
The formula for the Standard Gravitational Parameter is:
μ = M•G
where:
- μ is the Standard Gravitational Parameter for a body
- M is the mass of the body
- G is the Universal Gravity Constant.
Reference
- Wikipedia: https://en.wikipedia.org/wiki/Apsis