The Ballistic Flight Vertical Velocity calculator computes the vertical (y component) velocity in a ballistic flight at a time (t) after launch based on an initial velocity, launch angle, and the acceleration due to gravity.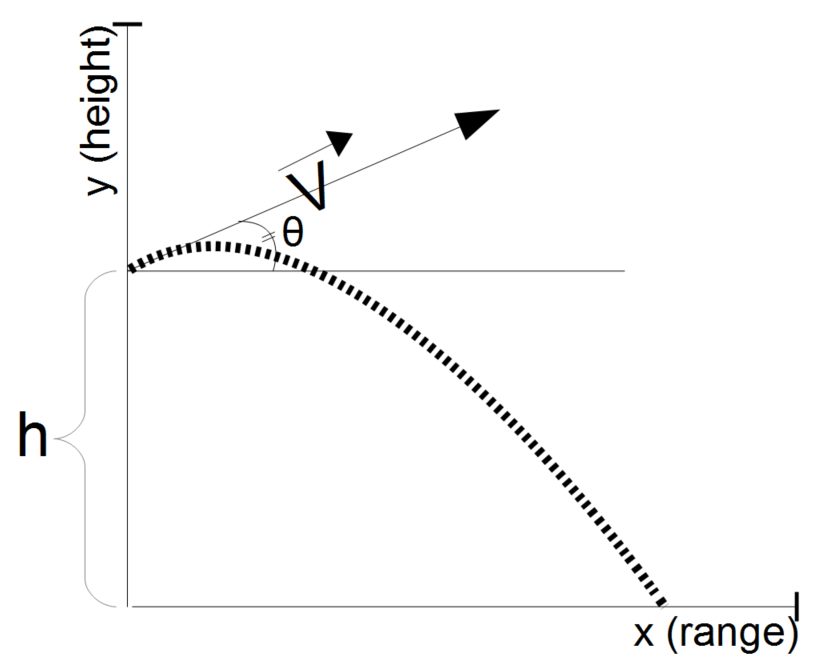
INSTRUCTIONS: Choose units and enter the following:
- (V0) Initial Velocity
- (Θ) Launch Angle
- (h) Height above Plane
- (t) Time into Ballistic Flight
Vertical Velocity (Vy): The calculator returns the vertical velocity in meters per second. However this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The Ballistic Vertical Velocity equation calculates an object's velocity in the y direction, the vertical component of its ballistic trajectory, at a given time. This is the equation for the ideal projectile, which means it neglects external forces such as air resistance. Since in the ideal projectile motion model the force of gravity is the only force component affecting the trajectory, and the force of gravity is parallel to the y-component of motion, the gravitational acceleration is the only affect the ballistic y-velocity. The y-component of velocity changes based on the time and the constant acceleration. The formula for the vertical velocity is:
where:
- Vy is the vertical velocity
- V0 is the initial velocity
- θ is the launch angle
- t is the time into the flight
- g is the acceleration due to gravity
Note: the height above the plane is used to determine the maximum flight time. If the entered time exceeds the maximum flight time, the vertical velocity at the time of impact is returned.
Ballistic Flight Calculators:
- Ballistic Maximum Altitude: This is the maximum altitude achieved in free ballistic flight.
- Ballistic Maximum Range: This is the maximum horizontal range.
- Ballistic Flight Time: This is the time duration of free flight.
- Simplified Ballistic Range: This is the range with no initial elevation above the plane.
- Ballistic Vertical Velocity: This is the vertical velocity at a given time.
- Ballistic Horizontal Velocity: This is horizontal velocity or ground speed.
- Vertical Position (Y) in Ballistic Flight: This compute the vertical position (y) at a given time within ballistic flight.
- Horizontal Position (X) in Ballistic Flight: This compute the horizontal position (x) at a given time within ballistic flight..
- Ballistic Position at Time (t): This compute the position (x,y) at a given time within ballistic flight, where x is distance down range and y is the height above the plane.
- Ballistic Parabolic Equation provides the parabolic flight position equation based on the launch speed, height and angle.
- Acceleration Due to Gravity at Sea Level
- Velocity to achieve a Max Ballistic Height: This computes the initial velocity required to achieve the max height.
- International Gravity Equation
- Force of Earth's Gravity
- Force of Drag
- ^ Young, Hugh and Freeman, Roger. University Physics With Modern Physics. Addison-Wesley, 2008. 12th Edition, (ISBN-13: 978-0321500625 ISBN-10: 0321500628 )Pg 81, eq 3.23
