Projectile Trajectory

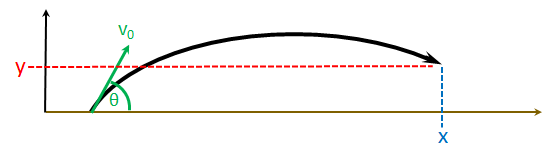
This equation computes the y value (altitude) of an object traveling on a ballistic trajectory given you know it's initial launch angle and the distance it has traveled in the x-direction (i.e., down-range).

The inputs to the equation are as follows:

• `v_0` - the initial velocity
• `theta` - the initial launch angle
• x - the location after some flight time

author: Andrew Budd

Notes

VISUALIZING THE TRAJECTORY

If you were to compute multiple values of y for multiple input values of x and plot them as x,y pairs on a Cartesian coordinate system, you would see the shape of the ballistic trajectory.  Remember that this ballistic trajectory is the path an object would take were it to be launched with a specified initial velocity and initial launch angle. Once launched it is assumed the only force acting on the object is the force of gravity, so this simplistic version of a ballistic trajectory neglects any affect of drag and other forces on the projectile.  This is an ideal ballistic trajectory applied to what could be pictured as a point mass.

ASYMPTOTE AT 90 DEGREES, X CAN ONLY BE ZERO

Notice that if you make the angle 90 degrees, in other words straight up, your input x value must be zero, as the projectile should go straight up and come straight down at the same point it was launched.  The only truly valid value for x as an input is zero. 

EXAMPLE:  If the angle, `theta`, is just slightly less than 90 degrees, let's say 89.999999996, the formula works correctly by computing the y-value when the projectile has ascended and then fallen sufficiently far for the small x-component drift to reach your specified value of x.

So, if you specify values such as `v_0` = 300 m/s, `theta`  = 89.999999996 degrees, and x = 100 m, the answer comes back a very large negative value -- meaning the projectile ascended to max altitude and then fell for a very long time while drifting in the x-direction at a very small constant x-velocity.