9.4 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
uniform circular motion — circular motion in which the magnitude of the velocity vector remains constant
nonuniform circular motion — circular motion in which the magnitude of the velocity vector changes
radial — parallel to the radius of a circle; the in-out direction
tangential — tangent to the circle, perpendicular to the radial direction
Notation
`a_r` — radial acceleration; the component of the acceleration vector along the in-out direction
`a_t` — tangential acceleration; the component of the acceleration vector tangent to the circle
Summary
If an object is to have circular motion, a force must be exerted on it toward the center of the circle. There is no outward force on the object; the illusion of an outward force comes from our experiences in which our point of view was rotating, so that we were viewing things in a noninertial frame.
An object undergoing uniform circular motion has an inward acceleration vector of magnitude
where `v=|v|`. In nonuniform circular motion, the radial and tangential components of the acceleration vector are
`a_r=v^2/r`
`a_t="slope of the graph of " v "versus" t`.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
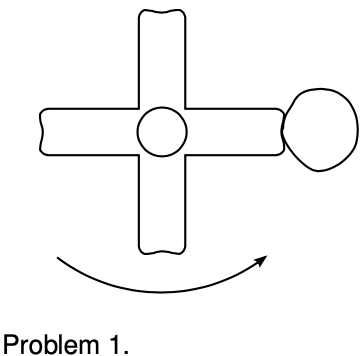 1. When you're done using an electric mixer, you can get most of the batter off of the beaters by lifting them out of the batter with the motor running at a high enough speed. Let's imagine, to make things easier to visualize, that we instead have a piece of tape stuck to one of the beaters.
1. When you're done using an electric mixer, you can get most of the batter off of the beaters by lifting them out of the batter with the motor running at a high enough speed. Let's imagine, to make things easier to visualize, that we instead have a piece of tape stuck to one of the beaters.
(a) Explain why static friction has no effect on whether or not the tape flies off.
(b) Analyze the forces in which the tape participates, using a table in the format shown in section 5.3.
(c) Suppose you find that the tape doesn't fly off when the motor is on a low speed, but at a greater speed, the tape won't stay on. Why would the greater speed change things? [Hint: If you don't invoke any law of physics, you haven't explained it.]
2. Show that the expression `|v|^2"/"r` has the units of acceleration.
3. A plane is flown in a loop-the-loop of radius 1.00 km. The plane starts out flying upside-down, straight and level, then begins curving up along the circular loop, and is right-side up when it reaches the top. (The plane may slow down somewhat on the way up.) How fast must the plane be going at the top if the pilot is to experience no force from the seat or the seatbelt while at the top of the loop `sqrt`
4. In this problem, you'll derive the equation `|a|=v^2"/"r` using calculus. Instead of comparing velocities at two points in the particle's motion and then taking a limit where the points are close together, you'll just take derivatives. The particle's position vector is `r=(rcostheta) hatx +(rsintheta) haty`, where `hatx` and `haty` are the unit vectors along the `x` and `y` axes. By the definition of radians, the distance traveled since `t=0` is `rtheta`, so if the particle is traveling at constant speed `v=|v|`, we have `v=rtheta"/"t`.
(a) Eliminate `theta` to get the particle's position vector as a function of time.
(b) Find the particle's acceleration vector.
(c) Show that the magnitude of the acceleration vector equals `v^2"/"r`. ? `sqrt`
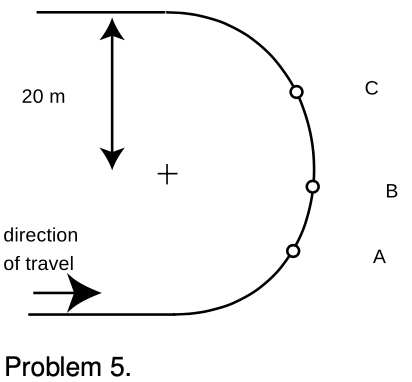 5. Three cyclists in a race are rounding a semicircular curve. At the moment depicted, cyclist A is using her brakes to apply a force of 375 N to her bike. Cyclist B is coasting. Cyclist C is pedaling, resulting in a force of 375 N on her bike. Each cyclist, with her bike, has a mass of 75 kg. At the instant shown, the instantaneous speed of all three cyclists is 10 m/s. On the diagram, draw each cyclist's acceleration vector with its tail on top of her present position, indicating the directions and lengths reasonably accurately. Indicate approximately the consistent scale you are using for all three acceleration vectors. Extreme precision is not necessary as long as the directions are approximately right, and lengths of vectors that should be equal appear roughly equal, etc. Assume all three cyclists are traveling along the road all the time, not wandering across their lane or wiping out and going off the road.
5. Three cyclists in a race are rounding a semicircular curve. At the moment depicted, cyclist A is using her brakes to apply a force of 375 N to her bike. Cyclist B is coasting. Cyclist C is pedaling, resulting in a force of 375 N on her bike. Each cyclist, with her bike, has a mass of 75 kg. At the instant shown, the instantaneous speed of all three cyclists is 10 m/s. On the diagram, draw each cyclist's acceleration vector with its tail on top of her present position, indicating the directions and lengths reasonably accurately. Indicate approximately the consistent scale you are using for all three acceleration vectors. Extreme precision is not necessary as long as the directions are approximately right, and lengths of vectors that should be equal appear roughly equal, etc. Assume all three cyclists are traveling along the road all the time, not wandering across their lane or wiping out and going off the road.
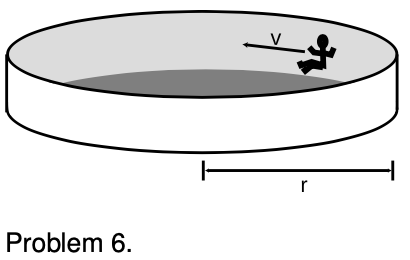 6. The amusement park ride shown in the figure consists of a cylindrical room that rotates about its vertical axis. When the rotation is fast enough, a person against the wall can pick his or her feet up off the floor and remain “stuck” to the wall without falling.
6. The amusement park ride shown in the figure consists of a cylindrical room that rotates about its vertical axis. When the rotation is fast enough, a person against the wall can pick his or her feet up off the floor and remain “stuck” to the wall without falling.
(a) Suppose the rotation results in the person having a speed `v`. The radius of the cylinder is `r`, the person's mass is `m`, the downward acceleration of gravity is `g`, and the coefficient of static friction between the person and the wall is `mus`. Find an equation for the speed,`v`, required, in terms of the other variables. (You will find that one of the variables cancels out.)
(b) Now suppose two people are riding the ride. Huy is wearing denim, and Gina is wearing polyester, so Huy's coefficient of static friction is three times greater. The ride starts from rest, and as it begins rotating faster and faster, Gina must wait longer before being able to lift her feet without sliding to the floor. Based on your equation from part a, how many times greater must the speed be before Gina can lift her feet without sliding down? `***`
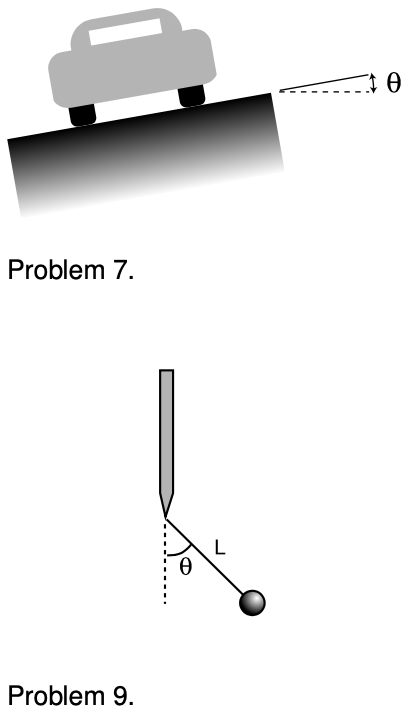 7. An engineer is designing a curved off-ramp for a freeway. Since the off-ramp is curved, she wants to bank it to make it less likely that motorists going too fast will wipe out. If the radius of the curve is `r`, how great should the banking angle, `theta`, be so that for a car going at a speed `v`, no static friction force whatsoever is required to allow the car to make the curve? State your answer in terms of `v`, `r`, and `g`, and show that the mass of the car is irrelevant.
7. An engineer is designing a curved off-ramp for a freeway. Since the off-ramp is curved, she wants to bank it to make it less likely that motorists going too fast will wipe out. If the radius of the curve is `r`, how great should the banking angle, `theta`, be so that for a car going at a speed `v`, no static friction force whatsoever is required to allow the car to make the curve? State your answer in terms of `v`, `r`, and `g`, and show that the mass of the car is irrelevant.
8. Lionel brand toy trains come with sections of track in standard lengths and shapes. For circular arcs, the most commonly used sections have diameters of 662 and 1067 mm at the inside of the outer rail. The maximum speed at which a train can take the broader curve without flying off the tracks is 0.95 m/s. At what speed must the train be operated to avoid derailing on the tighter curve? `sqrt`
9. The figure shows a ball on the end of a string of length `L` attached to a vertical rod which is spun about its vertical axis by a motor. The period (time for one rotation) is `P`.
(a) Analyze the forces in which the ball participates.
(b) Find how the angle `theta` depends on `P,g`, and `L`. [Hints: (1) Write down Newton's second law for the vertical and horizontal components of force and acceleration. This gives two equations, which can be solved for the two unknowns, `theta` and the tension in the string. (2) If you introduce variables like `v` and `r`, relate them to the variables your solution is supposed to contain, and eliminate them.] `sqrt`
(c) What happens mathematically to your solution if the motor is run very slowly (very large values of `P`)? Physically, what do you think would actually happen in this case?
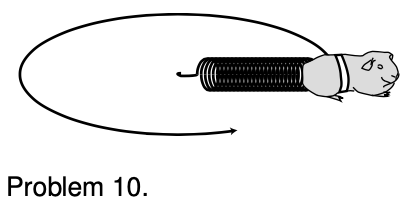 10. Psychology professor R.O. Dent requests funding for an experiment on compulsive thrill-seeking behavior in guinea pigs, in which the subject is to be attached to the end of a spring and whirled around in a horizontal circle. The spring has relaxed length `b`, and obeys Hooke's law with spring constant `k`. It is stiff enough to keep from bending significantly under the guinea pig's weight.
10. Psychology professor R.O. Dent requests funding for an experiment on compulsive thrill-seeking behavior in guinea pigs, in which the subject is to be attached to the end of a spring and whirled around in a horizontal circle. The spring has relaxed length `b`, and obeys Hooke's law with spring constant `k`. It is stiff enough to keep from bending significantly under the guinea pig's weight.
(a) Calculate the length of the spring when it is undergoing steady circular motion in which one rotation takes a time `T`. Express your result in terms of `k`, `b`, `T`, and the guinea pig's mass `m`. `sqrt`
(b) The ethics committee somehow fails to veto the experiment, but the safety committee expresses concern. Why? Does your equation do anything unusual, or even spectacular, for any particular value of `T`? What do you think is the physical significance of this mathematical behavior?
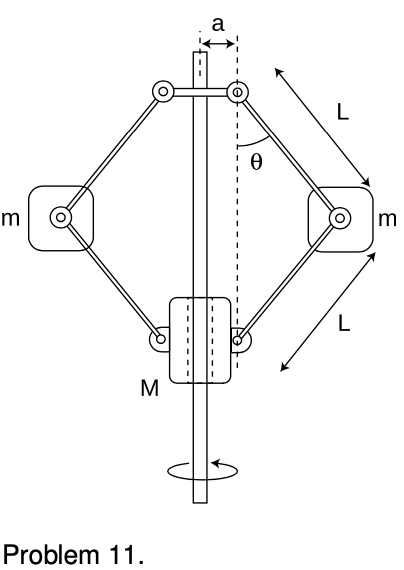 11. The figure shows an old-fashioned device called a flyball governor, used for keeping an engine running at the correct speed. The whole thing rotates about the vertical shaft, and the mass `M` is free to slide up and down. This mass would have a connection (not shown) to a valve that controlled the engine. If, for instance, the engine ran too fast, the mass would rise, causing the engine to slow back down.
11. The figure shows an old-fashioned device called a flyball governor, used for keeping an engine running at the correct speed. The whole thing rotates about the vertical shaft, and the mass `M` is free to slide up and down. This mass would have a connection (not shown) to a valve that controlled the engine. If, for instance, the engine ran too fast, the mass would rise, causing the engine to slow back down.
(a) Show that in the special case of `a=0`, the angle `theta` is given by
`theta=cos^(-1)((g(m+M)P^2)/(4pi^2mL))`,
where `P` is the period of rotation (time required for one complete rotation).
(b) There is no closed-form solution for `theta` in the general case where `a` is not zero. However, explain how the undesirable low-speed behavior of the `a=0` device would be improved by making `a` nonzero.
[Based on an example by J.P. den Hartog.] `***`
12. The figure shows two blocks of masses `m_1` and `m_2` sliding in circles on a frictionless table. Find the tension in 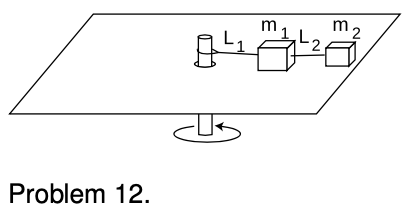 the strings if the period of rotation (time required for one rotation) is `P`. `sqrt`
the strings if the period of rotation (time required for one rotation) is `P`. `sqrt`
13. The acceleration of an object in uniform circular motion can be given either by `|a|=|v|^2"/"r` or, equivalently, by `|a|=4pi^2r"/"T^2`, where `T` is the time required for one cycle (example 6 on page 247). Person A says based on the first equation that the acceleration in circular motion is greater when the circle is smaller. Person B, arguing from the second equation, says that the acceleration is smaller when the circle is smaller. Rewrite the two statements so that they are less misleading, eliminating the supposed paradox. [Based on a problem by Arnold Arons.]
14. The bright star Sirius has a mass of `4.02×10^30 kg` and lies at a distance of `8.1×10^16 m` from our solar system. Suppose you're standing on a merry-go-round carousel rotating with a period of 10 seconds, and Sirius is on the horizon. You adopt a rotating, noninertial frame of reference, in which the carousel is at rest, and the universe is spinning around it. If you drop a corndog, you see it accelerate horizontally away from the axis, and you interpret this as the result of some horizontal force. This force does not actually exist; it only seems to exist because you're insisting on using a noninertial frame. Similarly, calculate the force that seems to act on Sirius in this frame of reference. Comment on the physical plausibility of this force, and on what object could be exerting it. `sqrt`
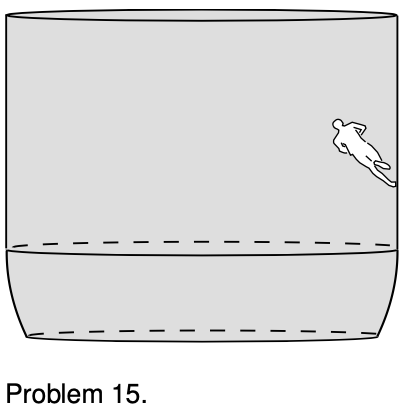 15. In a well known stunt from circuses and carnivals, a motorcyclist rides around inside a big bowl, gradually speeding up and rising higher. Eventually the cyclist can get up to where the walls of the bowl are vertical. Let's estimate the conditions under which a running human could do the same thing.
15. In a well known stunt from circuses and carnivals, a motorcyclist rides around inside a big bowl, gradually speeding up and rising higher. Eventually the cyclist can get up to where the walls of the bowl are vertical. Let's estimate the conditions under which a running human could do the same thing.
(a) If the runner can run at speed `v`, and her shoes have a coefficient of static friction `mus`, what is the maximum radius of the circle? `sqrt`
(b) Show that the units of your answer make sense.
(c) Check that its dependence on the variables makes sense.
(d) Evaluate your result numerically for `v=10 m"/"s` (the speed of an olympic sprinter) and `mu_s=5`. (This is roughly the highest coefficient of static friction ever achieved for surfaces that are not sticky. The surface has an array of microscopic fibers like a hair brush, and is inspired by the hairs on the feet of a gecko. These assumptions are not necessarily realistic, since the person would have to run at an angle, which would be physically awkward.) `sqrt`
9.4 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.