LM 9_3 Nonuniform circular motion Collection

9.3 Nonuniform circular motion by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

9.3 Nonuniform circular motion

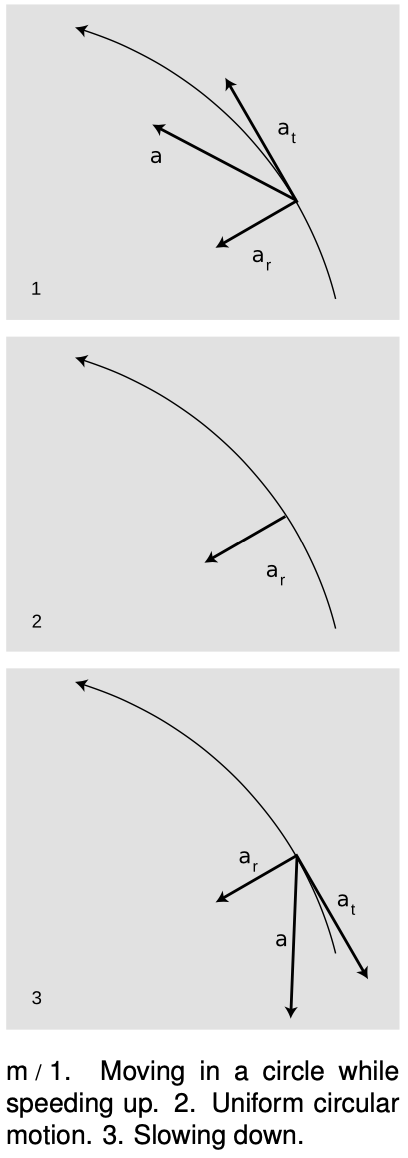
What about nonuniform circular motion? Although so far we have been discussing components of vectors along fixed `x` and `y` axes, it now becomes convenient to discuss components of the acceleration vector along the radial line (in-out) and the tangential line (along the direction of motion). For nonuniform circular motion, the radial component of the acceleration obeys the same equation as for uniform circular motion,

                                    `a_r=v^2"/"r`,

where `v=|v|`, but the acceleration vector also has a tangential component,

                                     `a_t="slope of the graph of"  v  "versus"  t`.

The latter quantity has a simple interpretation. If you are going around a curve in your car, and the speedometer needle is moving, the tangential component of the acceleration vector is simply what you would have thought the acceleration was if you saw the speedometer and didn't know you were going around a curve.

Example 9: Slow down before a turn, not during it.

`=>` When you're making a turn in your car and you're afraid you may skid, isn't it a good idea to slow down?

`=>` If the turn is an arc of a circle, and you've already completed part of the turn at constant speed without skidding, then the road and tires are apparently capable of enough static friction to supply an acceleration of  `|v|^2"/"r`. There is no reason why you would skid out now if you haven't already. If you get nervous and brake, however, then you need to have a tangential acceleration component in addition to the radial one you were already able to produce successfully. This would require an acceleration vector with a greater magnitude, which in turn would require a larger force. Static friction might not be able to supply that much force, and you might skid out. The safer thing to do is to approach the turn at a comfortably low speed.

`=>` Solved problem: A bike race — problem 5

9.3 Nonuniform circular motion by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.